Visata kaip kompiuteris
Taip pat skaitykite: Naujojo tipo mokslas
Fizikai jau ilgokai išsijuosę ieško Vieningos teorijos, leisiančios paaiškinti viską mūsų Visatoje. Jie spaudžia vyriausybes skirti milijardus el. dalelių greitintuvams (žr. Hadronų koliderio kūrėjas), tačiau, galbūt, jų ieškomas atsakymas yra mūsų kompiuteriuose. Ar tik nėra tąja paslaptimi tai, kad Visata viso labo tėra kompiuteris?
Pvz., S. Volframas, pasauliui davęs Mathematica programą, mano, kad skaičiavimas yra visa ko pagrindas. 2001 m. jis išleido knygą Naujasis mokslas, kurioje išdėstė savo mintis. Vieniems ji atvėrė akis, kiti mano, kad tai tik ankstesnių idėjų išdėstymas su tam tikra misticizmo doze.
Šiek tiek pristatysime pagrindines šios knygos idėjas. Tačiau pirmiausia būtina atsakyti į klausimą, o ką kompiuteriai turi bendra su mokslinėmis teorijomis?
Mokslinė kokio nors dalyko teorija yra tarsi kompiuterinė programa. Ji paaiškina reiškiniuose glūdinčius principus, kas tarsi supaprastina juos. Paimkime gravitaciją. Yra daugybė reiškinių, kuriuos reiktų aiškinti: obuoliai krenta ant galvos, Mėnulis sukasi aplink Žemę ir t.t., tačiau vieninga teorija (kad visa materija traukia viską) daug ką paaiškina.
Taigi, teorija yra paaiškinimas, kuris yra gerokai paprastesnis, nei pats aiškinamas reiškinys. Iš kitos pusės, teorija yra tarsi taisyklių ar instrukcijų rinkinys, nusakantis, kaip imituoti reiškinį (pvz., Mėnulio sukimąsi aplink Žemę). O štai kompiuterinė programa irgi yra taisyklių rinkinys, kuris sukuria tam tikrą kompiuterio elgesį, kuris gali būti gerokai sudėtingesnis, nei tikėjomės iš programos. Tokia esminė S. Volframo idėja, tiesa, ji išdėstyta per 1000 puslapių.
Tad ir Visata gali būti didelis kompiuteris, kuris vykdo programą, pateikiančia visa, ką matome aplink. Ši idėja turi du kontrargumentus. Vienas jų, kad gali nebūti vieningos teorijos, taigi ir programos. Tačiau tada kaip nustatyti, kas nutiks, kai susidurs dvi el. dalelės? O jei jau žinome, kas nutiks, tada jau turime analoginį kompiuterį.
Tačiau juk galite tiesiog pasakyti, kad tai, kas nutinka, tiesiog nutinka ir tam visai nebūtina logika. Ir tikroji problema yra tai, kad Visatoje tai, kas nutinka nėra tiksliai apibrėžta sąlygomis, esančiomis prieš tai nutinkant.
Turime paimti pačias paprasčiausias programas. Rinktis galime iš Tiuringo mašinos, gramatikų, rekursyvios logikos ir t.t., tačiau Naujajame moksle naudojami ląsteliniai automatai (CA). Jie ne tik įdomi programų rūšis, bet ir labai patraukli. Juos 5-me dešimtm. sukūrė S. Ulamas ir Dž. fon Neimanas, kai ieškojo save replikuojančių mašinų, turinčių gyvųjų organizmų požymius, kompiuterinių modelių.
Iš esmės, CA yra taisyklė, kurias agentai gali taikyti lokaliai. Galimas matematinis apibrėžimas ir kuo toks modelis pilnesnis, tuo sunkiau jį taikyti. Agentai yra tam tikru būdu sutvarkyti (dažnai, išdėstyti tinklelyje) ir paprastai tegali matyti tuos agentus, prie kurių yra netoliese; pats agentas paprastai gali būti tam tikroje būsenoje (dažnai, 1 arba 0). Kiekvienam agentui priskirta taisyklė, dažniausiai ta pati, apibrėžianti, kaip agentas gali pakeisti savo būseną, priklausomai nuo savo būsenos ir gretimų agentų būsenų. Dažniausiai signalu keisti būsenas yra laikrodžio tikas ar koks kitas įvykis, kurį gali pajusti visi agentai.
Jau turėtumėte atpažinti panašumą į gerai žinomą kompiuterinį žaidimą Gyvybė, kurį sumąstė John Conway. Kaip jis veikia, iliustruokime tokia pradine padėtimi. O taisyklė, kurią turi įvykdyti kiekvieno laikrodžio tiko metu, yra tokia: jei esi juodas ir turi baltą kaimyną, lieki juodu, o priešingu atveju virsti baltu. Kaimynas yra bet kuris agentas, esantis greta vertikaliai arba horizontaliai. Ir nustebsite, kad ši taisyklė palieka tik pradinės figūros juodą kontūrą.
 ===>
===>

Atkreipkite dėmesį, kad bet kuris agentas tenaudojo tik lokalią jam prieinamą informaciją ir vis tik gavome tai, kas gali būti laikomas kažkuo globaliu figūros kontūru. Taigi galime padaryti išvadą, kad labai paprasta taisyklė gali sukelti sudėtingą elgseną.
Tačiau toks dvimatis CA, kaip Gyvybė, yra pernelyg sudėtingas, kad jį būtų galima smulkiai
analizuoti. Tad S. Volframas nusprendė naudoti vienmatį CA. Kadangi tokie CA yra vienoje tiesėje, tai jų
veikimą lengviau atvaizduoti piešiant liniją po linijos. Taisyklę galime nurodyti remiantis gretimų
kaimynų spalva. Pvz., jei du balto taško abu kaimynai yra juodi, tai taškas virsta juodu:

Kadangi tėra tik 8 galimos kaimynų kombinacijos, tai taisyklė būtų taško spalva kiekvienai tų
kombinacijų. Koduodami juodą tašką kaip 1, o baltą tašką kaip 0, kiekvieną kombinaciją galime užrašyti
dvejetainiu skaičiumi, kurio reikšmė yra 0-7. Tarkim taisyklė gali būti tokia:
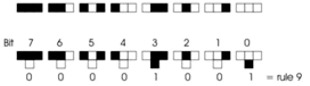
Tai reiškia, kad skaičiumi įvardinti galima visas 256 taisykles, kurios galimos vienmačiame CA. Tai kažkas iš konceptualaus sprendimo, nes tai leidžia klasifikuoti kiekvieną leistiną taisyklę. Ir būtent taip turėtų elgtis biologas, susidūręs su nauja biosfera. Kai tik suklasifikuojate tai, ką matote, galite pradėti matyti dėsningumus ir kurti teorijas. Be klasifikacijos tiesiog tik žiūrite į betvarkę, ir visai nesvarbu, kaip tai būtų įdomu.
S. Volframas ištyrė visas 256 galimas taisykles ir nustatė, kad jas galima suskirstyti į 4 klases pagal jų elgesį:
1 klasė yra nuobodi, nes rezultate gauname, kad visi taškai yra vienos spalvos;
2 klasė irgi nuobodoka, nes sukuria stabilias būsenas;
3 klasė yra netvarkingos elgesio atsitiktiniai trikampiai ir vaizdinis triukšmas;
 4 klasė yra sudėtingos elgsenos taisyklės, sudarančios į Gyvybę panašius darinius.
4 klasė yra sudėtingos elgsenos taisyklės, sudarančios į Gyvybę panašius darinius.
90 taisyklė sukuria įdomius pasikartojančius darinius. Taigi 1D CA yra gana įdomūs, nors vizualaus požiūrio gal ir ne tokie įdomūs, kaip fraktalai.
Toliau galima apibendrinti 1D CA, leidžiant taškams įgyti daugiau spalvų ne vien juodą ir baltą. Savo knygoje S. Volframas tvirtina, kad 2-ių būsenų 3-ių spalvų CA yra paprasčiausia universali Tiuringo mašina (įrodyta, kad ja nėra kad 2-ių būsenų 2-ių spalvų CA), ką 2007 m. ir įrodė Birmingemo un-to (Anglija) absolventas.
Ir tai pasiekiame, kas mus iš tikro domina kad nepaprastai paprasta taisyklė gali turėti labai sudėtingą elgesį ir būti kieno nors (jei tik ne visko!) teorija.
Visa klasikinė fizika ir dar daug kas remiasi diferencialinėmis lygtimis, kurios iš esmės nurodo, kaip vienas ar keli dydžiai kinta kaip kitų kintamųjų funkcija. Pvz. planetos orbita aplink Saulę gali būti paskaičiuota sprendžiant diferencialinę lygtį, kurioje greitis, t.y. jos pozicijos kitimo sparta, yra jos pozicijos Saulės atžvilgiu funkcija.
Tad galima tarti, kad diferencialinės lygtys yra taisyklės, kurias naudoja klasikinės ir šiuolaikinės teorijos, tad ryšis tarp jų ir CA būtų tikrai svarbus žingsnis, leisiantis svarbesnę CA padėtį. Dif. lygtys, sprendžiamos skaitmeniniais būdais, akivaizdžiai yra CA. Pvz., Laplaso lygtis gali būti išspręsta padalijant sritį į tinklelį ir priskiriant atsitiktines reikšmes, o tada taikant paprastą taisyklę: kiekvienoje celėje pakeisti reikšmę gretimų celių vidurkiu.
Tai tik patvirtina faktą, kad fizikoje gamtos dėsniai gali būti išreikšti arba diferencialinėmis, arba integralinėmis lygtimis. Dif. lygtys yra tarsi lokalios, nes apibūdina, kas vyksta taško kaimynystėje, o integralinės tarsi globaliomis, nes jos apibūdina, kas nutinka, kai viską susumuojame (t.y., suintegruojame). Tačiau ir dif. lygtys turi globalų pobūdį, nes turi tenkinti kontūro sąlygas.
Toliau pereikime prie atsitiktinumų. Tai didelė problema moksle (bendrai) bei taisyklėse (atskiru atveju). Vien pagalvokite, kaip deterministinis

Gyvūno oda, kurią generuoja CA |
Be jokių abejonių, kai siejasi su tokiomis idėjomis, kaip chaosas, informaciją ir sudėtingumo teorija. Atsitiktinumas atsiranda dviem būdais: a) iš atsitiktinių pradinių sąlygų; b) iš kai kurių taisyklių pobūdžio. Tik tai nėra nieko nauja, jei apsižvalgytume aplink.
Baigiamoji S. Volframo knygos dalis parodo, kaip CA idėja gali veikti ir kitose mokslo srityse. Aiškinama, kaip CA gali būti pritaikoma jūros kriauklių struktūroms, kaip gali sukurti kitokias biologines formas ir modeliuoti skysčių tekėjimą. Fizikos skyriuje randame kai kuriuos pasvarstymus apie diskrečius erdvės ir laiko aspektus, tačiau čia nėra nieko, kas leistų konkrečiai paskaičiuoti ar prognozuoti.
Taigi, ar tai yra revoliucija moksle, naujo tipo mokslas?
Svarbu nustatyti, kas yra ir kas nėra tiesa. Pirma, tai mokslas, nes tiria kai kurias labai sudėtingas sistemas labai klasikiniais metodais: eksperimentavimas, klasifikavimas ir aprašymas. Trūksta tik nuspėjimo. Tačiau tai nėra naujas mokslas, nes tuos klausimus jau seniai tiria sistemų sudėtingumo, CA, dirbtinio intelekto ir kitos teorijos.
O jei Visata yra didelis kompiuteris, kaip parašyti programą jam?
Taip pat skaitykite: Naujojo tipo mokslas
Poezija ir skaitiniai
Filosofijos sritis
HOT.LT svetainė
Vartiklis