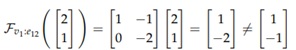1940 m. prancūzų matematikas ir artilerijos karininkas Jean Leray^*) pateko į vokiečių nelaisvę. Jis jiems pasakė, kad užsiima topologija, nes baiminosi, kad sužinoję jo tikrąją darbų sritį, hidrodinamiką, bus priverstas padėti vokiečiams. Per beveik 5-is įkalinimo metus tęsė tą apgaudinėjimą, užsiimdamas topologija ir galiausiai sukurdamas revoliucinę šiuolaikinės matematikos idėją – pėdo sąvoką, kuri, po to, kai A. Grothendieck’as ją 5-6 dešimtm. išpopuliarino, tapo pagrindiniu algebrinės geometrijos įrankiu.

Viename įvadiniame paaiškinime [jis sutrumpintai pateikiamas priede – labai rekomenduojame lygiagrečiai ir jį paskaityti >>>>] sakoma, kad į pėdus galima žiūrėti kaip plėtinius virš kitų matematinių objektų: „tarsi matematinis objektas tai žemės sklypas, o pėdas – daržas (ar dirbamas laukas) jame“. Pėdų pavadinimas (faisceaux) atsirado, nes jie turi „stiebų“ prijungimą prie po jais esančio objekto – ir tai priminė nupjautus ir surištus kviečių pėdus. Ir kaip daržai gali būti paruošiami įvairiose dirvose, taip pėdai gali būti „statomi“ ant įvairiausių matematinių objektų ir būti įvairių formų. Tačiau net patys paprasčiausi pėdai yra gana sudėtingi matematiniai dariniai.

Pabandykime sukurti vieną jų iš tiesių linijų. Paimkime realių skaičių tiesę:

Kuriame pėdą ne ant atskirų taškų joje, o ant intervalų. Tiesą intervalais galima suskaidyti begalybe skirtingų būdų, kurių vienas iš galimų parodytas čia:

Kiekviena skliaustų pora apima visus taškus, išskyrus kraštinius (tai atviri intervalai). Pėdas apima visus intervalus, ne tik vieną duotąjį. Kiekvienam intervalui gali būti priskirta „sekcijų“ aibė. Mūsų pavyzdyje sekcijos yra visos įmanomos atkarpos, kurios kerta intervalą. Paimkime tik vieną intervalą, kuriame iliustracijai pavaizduotos tik trys atkarpos (iš begalybės kitų):

Pėdą sudaro visų galimų intervalų visos galimos sekcijos ir intervalų junginiai, pvz.,

Tai gluminančiai chaotiškas darinys, tačiau matematiškai yra labai intriguojantis, nes savyje slepia bazinį paprastumą. Pateiktame pavyzdyje linijos praeina visaip, tačiau jos nesutampa.

Matematikus sudomino, kas nutinka, kai pasirenkama po vieną sekciją iš kiekvieno intervalo ir įvedamas reikalavimas, kad skirtingos sekcijos būtų suderinamos tarpusavyje taip, kad tarpusavyje derėtų persidengiantys intervalai. Jei intervalas randasi kitame, atkarpos privalo sutapti intervalų persidengime:

Iš šio lokalaus konstrukto išvedama globali pasekmė. Vietoje daugybės smulkių atkarpų gauname vienintelius galimus variantus, tenkinančius taisyklę: tiesės, kurios tęsiasi per visą skaičių ašį:

Šios vadinamos globaliomis sekcijomis. Būtent globalių objektų gavimas iš lokalių pėdams suteikia jų galią.

Virš realių skaičių tiesės galima sukurti daugybę pėdų. Tai tarsi kaip daug daržovių pasodinti darže. Tačiau tai tik pradžia. Vietoje to, kad sodintumėte kitą daržovę, jūs galite prižiūrėti kitą žemės sklypą. Įsivaizduokite, kad pėdą kuriate virš apskritimo, o ne virš linijos. Tada gauname struktūrą, atrodančią kaip begalinio aukščio cilindras. Objektų struktūra, nubrėžta ant šio cilindro, priklauso nuo konkrečios konstrukcijos konkrečiam pėdui.

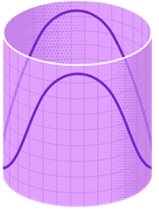
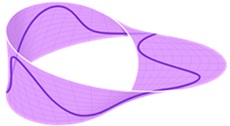
Iki šiol visi mūsų svarstomi pėdai gali būti laikomi kaip funkcijų šeimos. Tačiau pėdai gali būti (daug, žymiai labiau) sudėtingesni. Ankstesnės iliustracijos cilindras gali būti laikomas kilusiu iš begalinio aukščio stačiakampio, kurio šonai suklijuoti. Jei prieš klijuodami apsuktumėm stačiakampio galus, kaip parodyta kitame paveikslėlyje (negalima jos pavaizduoti begaline, kad parodome baigtinę Mobiuso juostą), sukurtumėte begalinio pločio Mobiuso juostą, kurioje vis dar galite nubrėžti grafikus primenančias kreives:

Bet kurioje lokalioje apskritimo dalyje ši kreivė atrodo kaip funkcijos grafikas. Tačiau globaliu mastu tai nėra funkcija, nes dėl pasukimo neįmanoma apibrėžti suderintos globalios koordinačių sistemos (jei keliaujate juosta, supratimas apie aukštyn ir žemyn galiausiai apsiverčia). Matematikai tokius objektus vadina „susuktomis funkcijomis“ (angl. twisted function).

Ir tuo metu, kai kiekvienas pėdas yra platus objektų rinkinys, galima nagrinėti ir visų pėdų virš duotojo matematinio objekto (realių skaičių tiesės, apskritimo ar kokios kitos matematinės esybės) aibę. Tai panašu į visus daržus, kuriuos galima įrengta duotame žemės sklype. Ir tai kažką pasako apie tai, kokia tai žemė. Kai kurie sklypai yra tropiniai miškai, o kiti – dykumos. Išsiaiškinimas to, kokie pėdai juose galimi, suteikia matematikams būdą ištirti struktūrą, sudarančią pagrindą erdvei, taip kaip ir žinojimas, kokie augalai auga tam tikrame dirvos tipe, suteikia žinių apie tą dirvą.

Pradedant Grothendieck’u matematikai pradėjo pamažu suprasti, kad pėdų aibės turi daug bendrumų su funkcijų rinkiniais, tik aukštesniame sudėtingumo lygmenyje. Galima sudėti ir dauginti pėdus ir net naudoti skaičiavimo metodų versiją. Tad būdamas nelaisvėje J. Leray atvėrė duris į visiškai naują matematikos pasaulį.

^*) Žanas Lerė (Jean Leray, 1906-1998) – prancūzų matematikas, dirbęs diferencialinių lygčių dalinėmis išvestinėmis bei algebrinės topologijos srityse. 1940  m. buvo patekęs į vokiečių nelaisvę, kurioje praleido 5 m., kartu su kitais belaisviais suorganizavęs universitetą (université en captivité). Stovykloje jis tęsė tyrinėjimus ir po išlaisvinimo paskelbė „Nelaisvėje dėstytą algebrinės topologijos kursą“ (1945). Tuo metu jis vengė diferencinių lygčių, baimindamasis, kad jų glaudus ryšis su taikomąja matematika gali priversti jį dirbti kariniams tikslams. Tad algebrinėje topologijoje užsiėmė spektrinėmis sekomis ir pėdais. Prie diferencialinių lygčių sugrįžo kažkur apie 1950-uosius. 1947-78 m. buvo College de France profesoriumi.

Pėdu galima laikyti būdu „pagerinti“ tam tikrą matematinio objekto rūšį. Galvokite apie matematinį objektą kaip žemės sklypą, o pėdą, kaip daržą jame. Tame sklype galima pasodinti skirtingų tipų daržus, o kartą pasodinę daržą, derliaus nuėmimas priklauso nuo to, koks daržas pasodintas [šias dvi dalis – įrengti daržą ir nuimti derlių – reikia turėti omenyje kalbant apie pėdus: jie turi struktūrą ir ką galima daryti toje struktūroje].

Norint sukurti pėdą ant matematinio objekto, reikia suprasti, kokie dalykai apipavidalina tą objektą ir kaip jie yra sutvarkyti. Grafai sudaryti iš briaunų, jungiančių taškus; topologinės erdvės sudarytos iš atvirų aibių. Bendra sąvoka nagrinėjant pėdus yra kryptis. Kai sakome, kad matematinis objektas turi tam tikrą „struktūrą“, į kurią turi atsižvelgti pėdas, paprastai turime omenyje kryptis, kuria visi dalykai yra vienas kitame. Grafo briaunos dažnai suprantamos kaip mazgų, kuriuos jungia, susikirtimai, tad grafe yra dalinė tvarka, kur e_ij < v_i, v_j briaunai e_ij, jungiančiai mazgus v_i ir v_j. Topologinėje erdvėje yra natūrali atvirų aibių tvarka. Jei aibė įeina į kitą, tvarka yra vienos aibės poaibis kitoje (U  V). Ta krypties prasme dažnai sakoma apie tai, kaip pėdas leidžia prijungti lokalius bei globalius duomenis prie objekto savybių [tarkim, galvokime apie lokalius duomenis kaip vieną obuolį, o globalius duomenis kaip visus obuolius nuo tos pačios obels].

Jei šį įvadinį tekstą padėsite greta kito, tik labiau matematiško ar abstraktaus, tai pėdai priima tą tvarką (lokalus-globalus) ir ją apverčia. Duomenys, prijungti prie didesnės objekto dalies turi būti suderinami apribojant ją į mažesnę dalį (globalus-lokalus). Tai galima įsivaizduoti kaip romano skaitymą. Jei yra potemė, užimanti vieną romano skyrių, tai veikėjų dialogai ir veiksmai atskirose pastraipose privalo turėti prasmę to skyriaus kontekste. Panašiai yra ir sakinyje toje pastraipoje. Tai dažnai vadinama patikslinimu ar skiriamosios gebos padidinimu.

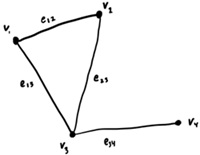
Dabar pereisime prie pavyzdžio. Tarkime turime grafą, kurio komponentės yra mazgai ir briaunos [briauną galima laikyti dviejų mazgų susikirtimu – tai leidžia grafą aprašyti aibių terminais, tad e_ij  v_i, v_j ]. Jos bus blokai pėdui F.

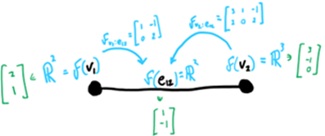
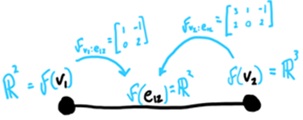
Pėdas turi du mechanizmus. Pirmasis paima komponentę ir priskiria jai naują erdvę, kuri vadinama stiebu. Tad mazgui v_i pėdas F jam priskiria, tarkim, realių skaičių vektorinę erdvę R, t.y. „pėdas virš v_i yra R“:
F(v_i)=R

Iš esmės, yra didelė laisvė, ką galima priskirti komponentei – praktiškai bet ką, kol komponentės dera tarpusavyje. Pvz., mazgams ir briaunoms priskirti skirtingų matavimų realių skaičių erdves (R², R²⁴ ir t.t.)

Antrasis mechanizmas reikalauja, kad „pėdai gerai derėtų tarpusavyje“, t.y. visi pėdai būtų pakankamai panašūs (pvz., būti Rⁿ), kad galėtume apibrėžti funkcijas tarp jų.

Taigi, pėdui F ir briaunai e_ij turimos dvi funkcijos iš abiejų mazgų į briauną, t.y.
F_vi;eij:F(v_i)->F(e_ij)
F_vj;eij:F(v_j)->F(e_ij)

Ir pėdas tokius atvaizdavimus turi kiekvienai briaunai ir susijusiems mazgams. Tie atvaizdavimai vadinami apribojimais pėdui F [jie vadinami apribojimais, nes apriboja kai kuriuos darinius mažesnėmis darinio dalimis, prisiminkime globalaus-lokalaus kryptis].

Grįžkime prie mūsų grafo ir tarkime, kad briaunai e₁₂ galioja F(v₁)=R²; F(v₂)=R³; F(e₁₂)=R²

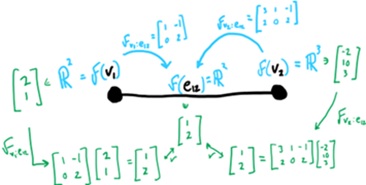
Kadangi kiekvienas stiebas yra vektorinė erdvė, tai natūralu apribojimus turėti kaip tiesines transformacijas, aprašomas matricomis. Kadangi sunku atvaizduoti visus pėdo stiebus, apsiribosime tik vienu:

Taigi, užbaigėme konstruoti pėdą! Literatūroje dažnai sutinkami Abelio grupių arba žiedų pėdai virš topologinių erdvių, nes jie pradžioje išrasti algebrinės topologijos kontekste, o tik vėliau pastebėti, kad naudingi algebrinėje geometrijoje.

O dabar pažiūrėkime, kaip galime panaudoti savo sukonstruotą pėdą.

Taigi turime vektorinės erdves, vadinamas stiebais, prijungtas prie kiekvieno grafo komponento. Tad paimkime kelis vektorius iš kiekvieno stiebo ir pažiūrėkime, kas nutiks. Vėlgi, iliustruosime tik grafo dalimi:

Elementų iš kiekvieno stiebo parinkimas vadinamas sekcija. Sumažinant abstrakcijos lygį, pėdą galime laikyto viena koherentine erdve, tada sekcija yra vienas tos erdvės elementas, taip kaip vektoriai yra vektorinės erdvės elementai ir taškai yra topologinės erdvės elementai.

Tad pažvelkime į mūsų pasirinktą sekciją. Panagrinėkime pirmąjį :

Matome, kad pasirinkimas stiebe F(v₁) yra nesuderinamas su pasirinkimu, nes

Panašiai yra ir su vektoriaus pasirinkimu F(v₂) stiebe. Tačiau įdomu, ar galima kiekviename stiebe pasirinkti vektorių taip, kad kiekvienai briaunai galiotų

kiekvieniems

t.y., vektoriaus pasirinkimas kiekviename stiebe būtų suderintas su jo vaizdu pagal jo apribojimus. Tai vadinama globalia sekcija. Terminas „globalus“ čia panaudojamas todėl, kad žiūrime į duomenis susietus visoje erdvėje ir matome, kaip jie išlieka derančiais, kai apribojami lokaliau. Pailiustruojame dalimi pėdo:

Globalios sekcijos yra svarbūs ir įdomūs duomenų tipai. Pėdas gali turėti vieną, begalinį arba baigtinį skaičių globalių sekcijų arba neturėti nė vienos. Praktiškai atsakoma į daug klausimų nustatant, kokia yra pėdo visų globalių sekcijų aibė – paprastai žymima G(F). Tai yra panašiai, kaip grupių homomorfizmui branduolys yra labiausiai dominantis dalykas.

Mūsų pavyzdys buvo vektorinių erdvių pėdas ant grafo. Tikėtiniausia, kad nesutiksite taip aiškinamų pėdų, tačiau, galbūt, šis pavyzdys padėjo geriau apčiuopti su pėdais susijusias idėjas. Daugumoje vadovėlių pateikiami Abelio grupių pėdai ant tolydžios topologinės erdvės. Mažiau susipažinusiam su matematika, tai gali būti sunkiau suvokti, tačiau vis tik pabandome pateikti ir tokį pėdo pavyzdį.

Topologinėje erdvėje X Abelio grupių pėdas kiekvienai atvirai aibei iš X priskiria Abelio grupę. Bet kokią Abelio grupę? Tai turi būti tolydžių funkcijų iš U į R grupė. Tad atvirai aibei U  R, stiebas iš U yra grupė F(U) := {f:U -> R}, kur f yra tolydi. Ir atvirai aibei V  U apribojimo atvaizdavimas F_U:V: F(U) -> F(V) yra iš tikro paprastas ir dažnai žymimas f|_V. Tad F_U:V yra homomorfizmas.

Atrodytų, kad nenaudinga turėti funkciją, atvaizduojančią į save mažesniame domene, tačiau paaiškinsime, kodėl pėdas sukonstruotas būtent taip.

Pirmiausia prisiminkime, kad topologinė erdvė yra virš R, tad kiekvienas stiebas atvirai aibei yra tolydžių funkcijų grupė iš R poaibio į R - o tai leidžia jas lengvai nubrėžti. Raudonos linijos yra kai kurie F(U) elementai (iš tikro, už U jie yra neapibrėžti).

Atvirai aibei V  U kiekvienos f F(U)) po F(U)_U:V vaizdai (raudonai pavaizduoti elementai iš F(U), o funkcijos vaizdas po F(U)_U:V, kuris yra F(V) elementas- mėlynai):

Kadangi dirbame algebriniu būdu, nėra analitinių manipuliacijų su funkcijomis, tad taškai U viduje, bet esantys V išorėje nėra į nieką atvaizduoti. Kiekviena funkcija yra jos elementas jos grupėje ir yra atvaizduojama į kitą elementą kitoje grupėje – tad tik taip nutinka, kad elementas ir jo vaizdas dėl šios homomorfizmo mums atrodo labai panašiai.

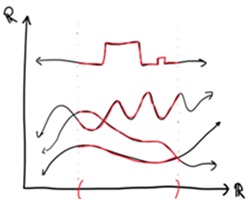
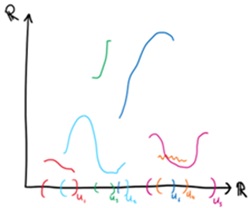
O kaip tada atrodo sekcijos? Sekcija yra elementų pasirinkimas kiekviename stiebe. Topologinėje erdvėje yra begalinis atvirų aibių skaičius, todėl ir begalinis stiebų kiekis. Tad sekcija yra vienos funkcijos iš F(U) kiekvienai atvirai aibei U (iš R) pasirinkimas. Pvz., fragmento iliustracija:

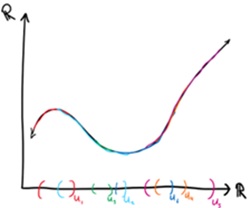
Bet vėl, kaip ir pirmame pavyzdyje, tai nelabai naudinga. Žaliai linijai (pavadinkime ją f₃) ir mėlynai linijai (pavadinkime ją f₂) F_U2U3(f₂)  f₃ - ir tai vienas iš nesuderinamumų toje sekcijoje. Tad vėl natūraliai sekantis žingsnis yra pažiūrėti kaip atrodo globali sekcija. Tai galėtų atrodyti kažkaip taip:

Tai nepaprasta! Mes aptarėme, kas turėtų vykti lokaliai ir iš tų taisyklių sukūrėme kažką globalioje struktūroje – tolydžią funkciją iš R į R. Tai galima buvo padaryti daugybe kitų būdų, tačiau taip lengviau brėžti, o taip pat lieka neįtikėtinas lankstumas kaip galima konstruoti pėdą ir kaip tas pėdas atrodytų. Todėl pėdai pasirodo įvairiose vietose ir turi įvairius jų panaudojimus – tiek algebrinėje geometrijoje, algebrinėje topologijoje, diferencialinėje geometrijoje, tiek ... tiesiog matematikoje!

Taip pat skaitykite:
Topologija
Begalybė (pristatymas)
Puankarė teiginio įrodymas
Vištų matematiniai pokalbiai
Skaičiai – apžvalga/ pradmenys
A. Whitehead. Skaičiavimų prigimtis
Kirmgrauža  tarp matematikos sričių
Mokslininkui  nereikia  matematikos!
Iš Antikos ateinantis klausimas: kiek jų?
M. Gardneris. Nė vienos pusės neturėjęs profesorius
Klasikinės „neišsprendžiamos“ geometrinės konstrukcijos
Naujos skaičių sistemos siekia atgauti pirminius skaičius
Egzotiškosios hipersferos - problema išspręsta
Žodžių anagramos, skaičiai, paprikos ir kt.
Endre Szemeredi darbų esmė „ant pirštų“
Kaip įmanomas begalinis klonavimas?
Diagramos, pakeitusios pasaulį
Kita skaičiavimo metodų istorijos pusė
Kombinatorika, polinomai, tikimybės
Trijų kūnų uždavinys aštuoniukėje
Visatos topologija: pradžiamokslis
Nauja pirminių skaičių klasė
Revoliucija mazgų teorijoje
Tūkstantmečio problemos
Trikampiai skaičiai
Matematikos keliu
Abelio premija
Erdvės formos