Mokslininkui nereikia matematikos!
Edward Osborne Wilsonas atskleidžia paslaptį: Atradimai kyla iš idėjų, o ne iš skaičiavimų.
Taip pat paskaitykite: Amerikai matematika nereikalinga!
Biologas E. O. Wilsonas knygoje Laiškai jaunajam mokslininkui teigia, kad nereikia būti stipriu
matematikoje, o aukštas IQ gali būti kliuviniu. Ir reikia siekti tikslų ten, kur kiti neina dėl lengvų pergalių.
Tokios iškilaus mokslininko mintys tik sukėlė sumaištį. Ir jis nenusiramino, o toliau kaitina atmosferą. The
Wall Street Journal 2013 m. balandžio 6 d. numeryje pasirodęs jo straipsnis Iškilus mokslininkas ¹
pasikaustęs matematikoje sukėlė klegesį matematikų tarpe.

Knygoje bei straipsnyje Wilsonas nurodo, kiek daug žinomų šiuolaikinių mokslininkų buvo mažaraščiai matematikoje ir atskleidžia kaip jis, jau 32 m. amžiaus Harvardo profesorius, sėdo su paskutinių kursų studentais (pora jų - jo paties) mokytis skaičiavimo metodų ir, užgniaužęs savo išdidumą, pasiekė neišskirtinį C lygį. Mat mokslus pradėjęs gana prastose pietų mokyklose, jis nesimokė algebros, kol neįstojo į Alabamos un-tą. Dabar jis įsitikino, kad aukštesniosios matematikos sugebėjimai yra panašūs į užsienio kalbų mokėjimą. Galima jas geriau išmokti įdedant daugiau pastangų ir bendraujant su tais, kuriems ta kalba yra gimtoji. Tačiau daugumą laiko skiriant kitiems dalykams, pažanga nėra didelė.
Laimei, išimtinių matematinių sugebėjimų reikia tik keliose disciplinose, kaip kad el. dalelių fizikoje, astrofizikoje ir informatikoje. Kituose moksluose yra svarbiau sugebėjimai suformuluoti koncepcijas, kai manipuliuojama vaizdiniais bei vadovaujamasi intuicija.
Kiekvienas kartais pasvajoja kaip mokslininkas. Suvaldytos fantazijos yra bet kokio kūrybinio mąstymo šaltinis, Niutojas sapnavo, Darvinas sapnavo, visi sapnuoja. Pirmiausiai iškyla vaizdai. Jie gali keisti formą ir nublankti. Jie tampa patvaresni, kai išreiškiami diagramomis ant popieriaus ir įgauna savo gyvenimą kaip realūs surasti pavyzdžiai.
Mokslo pirmeiviai retai padarydavo atradimus remdamiesi grynąja matematika. Jų nuotraukos prie lentos su formulėmis yra apie jau padaryto atradimo paaiškinimai. Tikras atradimas atėjo kitiu metu, - laukuose darant užrašus, prie popieriaus užversto stalo, bandant kažką paaiškinti draugui ar valgant pietus.
Idėjos moksle kyla, kai kuri nors pasaulio dalis tiriama savo paties labui. Jos atsiranda iš visų turimų žinių ar iš įsivaizuotų esybių. Kai kažkas užčiuopta, tolimesni žingsniai dažniausiai reikalauja statistinių metodų, kurių pagalba atliekama tolimesnė analizė. Jei tai per sunku pačiam mokslininkui, į pagalbą pasitelkiamas matematikas ar statistikas.
20 a. 8-me dešimtm. Wilsonas dirbo su matematiku George Osteriu, nustatinėdami vabzdžių pasiskirstymą į kastas ir socialinį gyvenimo principus. Wilsonas pateikdavo surastus faktus, o Osteris panaudojo matematinius metodus tų reiškinių tyrimui. Neturėdamas faktinės informacijos, Osteris galėjo sukurti bendrąją teoriją, tačiau iš jos nebūtų padarytos išvados apie tai, kas iš tikro vyksta žemėje.
Per daugelį darbo su matematikais metus jis išvedė principą: daug lengviau mokslininkui rasti bendrą kalbą su matematikais, nei matematikams rasti mokslininkus, gebančius panaudoti jų teorijas. O antrasis jo principas būtų: Kiekvienam mokslininkam yra disciplina, kurioje jo matematinės kompetencijos lygis yra pakankamas, kad būtų pasiektas meistriškumas.
Wilsono tikslas nėra atgrasyti, o paskatinti galimai talentingus mokslininkus, kuriems nesiseka su skaičiais. Smegenų pajėgumai gali tapti sąjungininku.
Kai kurie patarimai yra labai pragmatiški nesusigundyk sritimis su švytinčia aura, o eik į ten, kur vyksta mažiausiai veiksmo. Kai kurie patarimai skamba tarsi erezija, tačiau juose yra prasmės: užmiršk avilio mąstymą ir leisk vienišam protui klajoti bei svajoti. Kai kurie atrodo įtartinai: Tikri mokslininkai niekada neatostogauja...
Aišku, kai kurie, persisotinę ir egocentriški, su juo tikrai nesutiks. Tačiau Wilsonas turi patarimą ir jiems pabrėždamas, kiek dar daug pasaulyje neištirta. Jūs reikalingi, - jis ramina.
Ir jis sako: Mokslininkas yra iš dalies poetas, ir naujais būdais išreikšdamas senas tiesas, poetas yra iš dalies mokslininkas.
Save nuomonę galite išsakyti šiame puslapyje.
Dr. Wilsonas yra Harvardo un-to garbės profesorius. Iš jo daugelio knygų paminėtinos Apie žmogaus prigimtį bei Socialinis Žemės užkariavimas.
Aukštoji matematika galima ir už grotų
 Kristoferis Cheivensas (Christopher R. Havens) - amerikiečių matematikas. Vaikystėje
rodė gabumus matematikai, tačiau anksti metė mokyklą, ėmė vogti, patekdavo į kalėjimą, buvo benamis, įjunko
į narkotikus. 2010 m. kovą per Olimpiadą nušovė narkotikų prekeivį. Nuteistas kalėti 25 m., kalėjime susimušė
su kitu nuteistuoju, už ką buvo įkalintas vienutėje. Toje skylėje (kaip pats sako) pradžioje užsiėmė sudoku,
vėliau ėmėsi spręsti matematinius uždavinius, kurie buvo šviečiamųjų priemonių dalimi; lankė matematikos užsiėmimus.
Tačiau jam trūko vedlio ir 2013 m. sausį kreipėsi pagalbos į pagrindinių matematinių žurnalų redaktorius.
Tai suvedė jį su Turino un-to prof. Umberto Cerruti; jis ir kiti matematikai jį aprūpino literatūra. Jų bendradarbiavimas tęsėsi
grandininių trupmenų srityje. 2016 m. kalėjimo administracija
nusprendė pradėti kartu su juo Kalėjimo matematikos projektą (PMP), kuriame pradėjo dalyvauti kaliniai iš viso pasaulio jis mokė matematikos
kitus nuteistuosius, o jam leido susidaryti nuosavą specializuotą biblioteką. Dabar jau ir jo dalyviai skelbia savo matematinius straipsnius.
Kristoferis Cheivensas (Christopher R. Havens) - amerikiečių matematikas. Vaikystėje
rodė gabumus matematikai, tačiau anksti metė mokyklą, ėmė vogti, patekdavo į kalėjimą, buvo benamis, įjunko
į narkotikus. 2010 m. kovą per Olimpiadą nušovė narkotikų prekeivį. Nuteistas kalėti 25 m., kalėjime susimušė
su kitu nuteistuoju, už ką buvo įkalintas vienutėje. Toje skylėje (kaip pats sako) pradžioje užsiėmė sudoku,
vėliau ėmėsi spręsti matematinius uždavinius, kurie buvo šviečiamųjų priemonių dalimi; lankė matematikos užsiėmimus.
Tačiau jam trūko vedlio ir 2013 m. sausį kreipėsi pagalbos į pagrindinių matematinių žurnalų redaktorius.
Tai suvedė jį su Turino un-to prof. Umberto Cerruti; jis ir kiti matematikai jį aprūpino literatūra. Jų bendradarbiavimas tęsėsi
grandininių trupmenų srityje. 2016 m. kalėjimo administracija
nusprendė pradėti kartu su juo Kalėjimo matematikos projektą (PMP), kuriame pradėjo dalyvauti kaliniai iš viso pasaulio jis mokė matematikos
kitus nuteistuosius, o jam leido susidaryti nuosavą specializuotą biblioteką. Dabar jau ir jo dalyviai skelbia savo matematinius straipsnius.
Jis užsiėmė klausimu kaip grandininė trupmena f bus transformuojama veiksmu (af + b) / (cf + d)? Nors šio klausimo sprendimas dar neatrastas, K. Cheivensas rado formules tam tikrai transformacijų klasei ir tai atliko rankiniu būdu, nes negalėjo naudotis kompiuteriu; tad tai jam truko dvejus metus, nes tos ilgos grandininės trupmenos nusidriekė per 4,5 m ilgio sąsiuvinio lapus, kuriais buvo išklijuotos jo kameros sienos..
2020 m. K. Cheivensas, U. Čerutis ir kiti dalyviai žurnale Skaičių teorijos tyrinėjimai paskelbė savo išvadas, aptikę, kad kai kurie hiperbolinės geometrijos objektai perteikiant grandininėmis trupmenomis sudaro tam tikras simetrijas. Netrukus po to U. Čeručio dukra Marta parašė trumpą straipsnelį apie mokslinio darbo sunkumus kalėjimuose, kuris patraukė dėmesį; nuteistieji negali naudotis kompiuteriais (LaTeX formules rašo be kompiuterių!), PMP sukūrė metodą kaip sudėtingus skaičiavimus jie galėtų atlikti naudodami jiems leistiną el. paštą (Jpay) - bet el. laiško išsiuntimas kaliniams kainuoja 50 centų, o jie vidutiniškai per valandą vidutiniškai uždirba 52 centus (ir dar draudžiama siųsti užkoduotus laiškus).
Vėliau su juo susisiekė ir Kalifornijos un-to kriptografas Amit Sahai. Paskutiniu metu jis dirba su periodinių grandininių trupmenų teleskopavimu ir rengia vadovėlį apie grandinines trupmenas. Jis sako, kad nori pakeisti kalėjimų kultūrą, tačiau supranta, kad tai aukšta kartelė.
Taip pat jis su vokiečiu matematiku Carsten Elsneriu užsiima grandininėmis funkcijomis, kuriose vidiniai skaičiai
yra 1, 2, 3,
- jas pavadino Zoft (vok. pynė, kasa) ir bando įrodyti, kad kad apskaičiuojant didžiausią bendrą
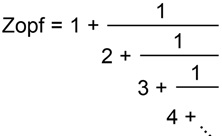 daliklį tarp vis tikslesnių Zopfo aproksimacijų fragmentų, gaunamas išsidėstymas, kuriame seka 1, 2, 3,...
kaitaliojasi su vienetų seka: 1, 1, 1, 2, 1, 3, 1, 4,...
daliklį tarp vis tikslesnių Zopfo aproksimacijų fragmentų, gaunamas išsidėstymas, kuriame seka 1, 2, 3,...
kaitaliojasi su vienetų seka: 1, 1, 1, 2, 1, 3, 1, 4,...
Tačiau tas pavadinimas turi ir simbolinę reikšmę. Vokiečių tautosakoje keliaujantis didikas įkrenta į pelkę, grimzta vis giliau ir giliau, kol purvas grasina jį visai praryti. Norėdamas ištrūkti, jis išsikapsto iš pelkės savo kasa. Elsneris pasiūlė Zopf dėl to, kad skaičiai sukasi aplink realių skaičių liniją, - bet, tam tikra prasme, K. Cheivensas gyvenimas panašia vingiuota linija iš pelkės nuvingiavo per matematiką atgal į gyvenimą.
Aplankykite Matematikos kalėjimuose projektą
Etnomatematika ir matematikos mokymas
A.J. Bishopas1) pabrėžė skirtumą tarp M(atematikos) ir m(atematikos). M yra toji, kurią žinome kaip mokslinę discipliną; kitaip tariant tai matematikų ir labai specializuotų fizikų bei inžinierių matematinės žinios. Tuo tarpu m yra kasdieniame gyvenime naudojami sugebėjimai skaičiuoti, matuoti ir pan. Abi kažkiek persidengia, tačiau bendrai imant ryšis tarp M ir m nėra aiškus. Dar aštresnis klausimas dėl jų kyla mokant matematikos: ar reikia visus mokyti M, ar apsiriboti tik m.
Iš dalies dėl gilėjančios krizės matematikos mokyme ir iš dalies dėl problemų matematikos pagrindų
absoliutistiniuose požiūriuose, į matematikos sritį skverbiasi natūralistinė matematikos teorija. Absoliutistinis
požiūris (formalizmas, logicizmas ir konstruktyvizmas) tvirtina, kad M žinios yra a priori ir nedisputuotinos. Pagal jį
matematiškai teisingi teiginiai visada deduktyviai išvedami iš a priori ar pateiktų teiginių. Pagal jį empirinė tikrovę į tai neįsikiša.

Todėl ir matematikos mokymas turėtų įtraukti mokinius į deduktyvų ir fundamentaliai dekontekstualizuotą (ir nesusietą su tikrove) matematinį mąstymą. Idealiu atveju, reikia pradėti mokyti koncepcijų ir procedūrų priklausančių matematikos pastato pamatams (pvz., aibių teorijos) ir palaipsniui kilti į kitas pakopas (t.y., aritmetika, algebra ir t.t.). Vadinamoji Moderniosios matematikos filosofija yra radikaliausia šio požiūrio forma. m koncepcijos ir procedūros laikomos netikusia matematika, klaidingomis procedūromis ar bent jau iki-moksline M versija. Visa tai privalo būti išskirta ir mokymo metu pakoreguota.
Pamažu vystosi alternatyvus požiūris į M. Absoliutistinių požiūrių nesėkmė (pradedantGiodelio įrodymu) ir didėjantis matematinio mokymo programų irimas leido iškilti labiau natūralistinėms teorijoms. Viena teorija tvirtina, kad į matematiką reikia žiūrėti kaip į iš esmės simbolinę technologiją, besiremiančią kultūrinės prigimties sugebėjimais arba aplinkos veikla. Kitą teoriją vadina etnomatematika. Natūralistinio požiūrio atstovai tvirtina, kad matematinio pažinimo ištakos yra pažįstančiojo kultūriniame kontekste. Pažinimas bendrai (ir atskiru atveju matematinis) yra kultūrinis ir kontekstualus iš prigimties. To pasekmė yra ta, kad M (šiaip, ne triviali) kuriama ir valdoma m koncepcijų ir intuicijų: empiriniai faktai, argumentai ir net asmeninės kultūros veiksnios procedūros suteikia realius M kontekstinius pagrindus.
Tada automatiškai kyla klausimas: kokia toji m? Mūsų pasaulyje visose žinomose kultūrose žmonės užsiima veikla susijusia su formaliomis ar matematinėmis žiniomis. A. Bishopas išskyrė 6 veiklos tipus: skaičiavimas, vietos erdvėje nustatyas, matavimas, braižymas, žaidimas ir aiškinimas. Skirtingose kultūrose tomis veiklomis užsiimta skirtingai ir jų studijos gali padėti atskleisti jose turėtus matematinius įgūdžius.
Laikui bėgant buvo atlikta įvairių tyrinėjimų skirtingose kultūrose. Tarp ankstyvųjų darbų paminėtini K. Zaslavskos apie
skaičiavimą Afrikoje (1973) bei J. Needhamo monumentalus veikalas apie algebrą bei geomanciją senovės Kinijoje
(1965). O D. Lancy pateikia įdomios informacijos apie Naująją Gvinėją (1983), R. Pinxtenas ir kt. apie erdvinį suvokimą ir
formų teoriją pas navahų indėnus (1983; 1987).
Taip pat skaitykite:
Australijos aborigenų matematikos samprata,
Prometėjo pėdsakas,
Matematika Egipte ir Finikijoje,
Išango kaulas,
Kas tie romėniški skaitmenys?
Pirmuoju išsamiu šios srities veikalu yra M. Ascher2) Etnomatematika (1991). Būdama matematike, ji pasirinko koncepcijas, kurios atrodė svarbiausiomis ir tuo aspektu vertina kitų kultūrų veiklas ir žinias. Ji parodo kaip operuojama skaičiais stebimuose kultūriniuose reiškiniuose. Tas pat yra su grafikais, geometriniais ornamentais, šeimos ryšių logika...
M. Ascher darbo svarba dvejopa: a) ji kultūrinius ir psichologinius aspektus panaudoja kaip būdus matematinių problemų aiškinimuisi; b) nurodo stiprų ryšį tarp M ir m (kai sociologai paliečia tik m).
Navahų erdvėformos
Navahams pasaulis yra labai dinamiškas: praktiškai jis buvo vien judėjimas ir kitimas. Tai skiriasi nuo mūsų pasaulio, kuris susideda iš situacijų ir objektų. Tai atsispindi ir jų kalboje, kurioje beveik viskas išreiškiama veiksmažodžiais. Pvz., žodis vykti jungiamas ne mažiau nei 300 tūkst. būdų. Miriadais būdų aprašoma, kaip veiksmas prasideda, baigiasi, kartojasi ir pan. Tuo pačiu navahai savo pasaulėžiūroje nesinaudoja dalies-visumos logika. Tuo tarpu vakariečiai pasaulį suvokia kaip visumą, sudarytą iš atskirų dalių. Taip yra ir matematikos suvokime, pvz., aibių teorijoje išskiriama aibė (visuma) ir elementai (dalys) kartu su specialiomis operacijomis; tiesė yra ją sudarančių taškų aibė ir t.t. Tuo tarpu navahai neturi tokio dalies-visumos samprotavimo.
Kita navahų ypatybe yra tai, kad erdvės ir formų koncepcijos beveik visada apibrėžiamos judėjimais ar poslinkiais: riba ar kraštas yra ne linija, o kliūtis, kuri keičia judėjimą; atstumai suprantami judėjimo terminais ir kraštovaizdžio ypatybėmis. Tai kaip navahų vaikams suprasti euklidinę geometriją?! Esmine yra vizualizacija.
Ir čia vienu erdvės elementų yra hoganas (tradicinis namas), kosminis pasaulio modelis, iliustruojantis navahų aukštyn-žemyn, proporcijų, vėjų kryptis ir pan. koncepcijas. Hoganas yra ir didaktinis instrumentas, pvz., leidžiantis vaikams suprasti orientacijos ir proporcijos sąvokas.
Literatūra:
- Claudia Zaslavsky. Africa Counts, 1973
- Joseph Needham. Science and Civilization in China// Cambridge University Press, vol.3, 1965
- David F. Lancy. Cross-cultural Studies in Cognition and Mathematics, 1983
- Rik Pinxten & oth. Anthropology of Space: Explorations into the Natural Philosophy and Semantics of Navajo Indians, 1983
- Rik Pinxten & oth. Towards a Navajo Indian Geometry, 1987
- Marcia Ascher. Ethnomathematics, A Multicultural View of Mathematical Ideas, 1991.
1) Alanas Bišopas (, g. 1937 m.) anglų ir australų matematikos pedagogas, kembridžo un-to ir Monašo un-to (Australija) profesorius. 1977 m. viešėdamas Papua Naujojoje Gvinėjoje susidomėjo kultūriniu matematikos pagrindu, savo studijas įkūnijęs knygoje Matematinis įkultūrinimas (1988). 1979-89 m. buvo H. Freudenthalio įsteigto žurnalo Matematikos edukacinės studijos redaktoriumi. 2015 m. gavo F. Kleino medalį, skiriamą už pasiekimus matematikos dėstymo srityje.
2) Marcia Alper Ascher (1935-2013) - amerikiečių matematikė. Nuo 1960 m. dėstė matematiką Ithaca koledže, kur buvo viena iš matematikos fakulteto įkūrėjų. Koledžą paliko 1995 m. Bendradarbiavo su vyru jo archeologiuose darbuose tiek JAV, tiek užsienyje. Jos 3 knygos buvo vienomis pirmųjų aptariant matematikos kultūrines tradicijas ir tradicijas: Quipu kodas (1981, kartu su R. Ascher), Etnomatematika (1991), Matematika visur: idėjos kultūrose (2002).
Papildomai skaitykite:
Ar viskas čia taip?
Pi keliai ir klystkeliai
Matematika ir biologija
Ar delfinai moka matematiką?
Amerikai matematika nereikalinga!
Kaip įmanomas begalinis klonavimas?
Matematikos ir fizikos šmaikštumai
Lietaus uždavinys ir matematinis mąstymas
Iš Antikos ateinantis klausimas: kiek jų?
Šriodingerio katinų dresiravimas: kvantiniai kompiuteriai
Naujos skaičių sistemos siekia atgauti pirminius skaičius
Paradoksai sulig dirbtiniu intelektu
Matematikos filosofinės problemos
Tribologija ir tepimo sprendimai
Trijų kūnų uždavinys aštuoniukėje
Meilės ir matematikos ritualai
Galilėjus, Dievas ir Matematika
Matematikos pradžia Lietuvoje
P. Karvašas. Archimedas
Kokiu greičiu skriejame?
Mažosios saulės mįslės
Matematikos keliu
Vartiklis