Parabolės lenktas likimas Čia pateikiami grynai matematiniai parabolės aspektai. Apie kitus parabolės panaudojimus skaitykite R. Kudžmos paskaitos konspekte Pasaulių begalybė,... paraidžiui, pasauliai be pabaigos Kūgių pjūviai yra tarp anksčiausiai tirtų kreivių. Tai kreivės, kurios gaunamos kūgį kertant
plokštuma. Kertant plokštuma lygiagrečia kūgio pagrindui gauname apskritimą, kai nuožulniai kerta
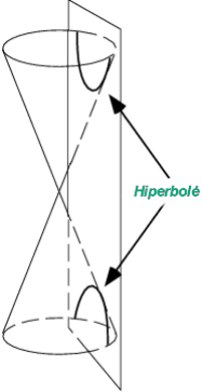
vieną kūgį - elipsę arba parabolę, kai iškart abi dvigubo kūgio dalis - hiperbolę. Kūgius nagrinėjo jau Menaechmas (375-325 m. pr.m.e.), buvęs Platono ir Eudokso mokiniu. Jis bandė išspęsti garsiąją kubo tūrio padvigubinimo problemą. Kūgius nagrinėjo ir Euklidas (325-265 m. pr.m.e.) bei Apolonijus (262-190 m. pr.m.e.). Pastarasis rezultatus apibendrino traktate Apie kūgius (Konikės), kurį sudarė 8 knygos, turinčios 487 teiginius. Apolonijus gautus rezultatus taikė planetų judėjimui aprašyti. Ir, atrodo, jis buvo pirmasis panaudojęs terminus elipsė, parabolė ir hiperbolė, nors paskutiniu metu tuo suabejota. Parabolės židinys ir direktrisė buvo Papuso tyrinėjimų objektas. Renesanso laikotarpiu Keplerio nustatyti planetų judėjimo dėsniai, Dekarto ir Ferma koordinačių geometrija bei G. Desargues4), La Hire ir Paskalio (parabolę nagrinėjęs kaip apskritimo projekciją) sukurtos projekcinės geometrijos užuomazgos kūgių savybių nagrinėjimus pakėlė į naują lygį. Galilėjus parodė, kad mesti kūnai veikiami gravitacijos brėžia paraboles. Gregory ir I. Niutonas aptarė parabolės savybę lygiagrečius spindulius nukreipti į židinį. Tarp kitų tyrinėtojų reikia paminėti Dandeliną, Gergonne, Ponceletą, Brianchoną, Dupin,ą Chasles ir Šteinerį. 1602 m. J. Kepleris pasakė tikįs, kad Marso orbita yra ovalo formos ir vėliau įrodė, kad ji elipsė su Saule viename židinių. Planetų ekscentriškumas yra nedidelis, pvz., Marso - 1/11, o Žemės - 1/60. 1705 m. E. Halley nustatė, kad jo atrasta kometa juda elipse. Jos ekscentriškumas 0.9675. Bet tik I. Niutonas įrodė, kad, veikiami gravitacijos, dangaus kūnai juda kūgio pjūvių kreivėmis: apskritimais, elipsėmis, parabolėmis ir hiperbolėmis. Kūgis Kad kūgio tūris yra lygus pagrindo plotui padaugintam iš trečdalio aukščio, pirmasis nustatė
Eudoksas, o įrodymus vėliau pateikė Archimedas
(Apie sferą ir cilindrą, apie 225 m. pr.m.e.) ir
Euklidas (Elementų teiginys XII.10): Kūgio šono aukštis: Kūgį galime apibrėžti tokiomis parametrizuotomis lygtimis: Kūgio paviršiaus plotas (be pagrindo): Parabolė Dekarto koordinačių sistemos bendroji parabolės lygtis
yra kvadratinė lygtis Apibrėžimas. Tiesei D (direktrisei) ir jai nepriklausančiam taškui F, vadinamam židiniu, parabolė yra visuma taškų P, nubrėžiamų plokštumoje taip, kad atstumas tarp P ir F lygus atstumui tarp P ir D. Židinio atstumas nuo direktrisės yra Paviršius, gautas sukant parabolę aplink jos simetrijos ašį, vadinamas paraboloidu. Parabolės, kurios šakos nukreiptos į dešinę, o viršūnė yra taške (0,0), lygtis Dekarto koordinačių
sistemoje yra |
  
|
|
Dydis 4a dar vadinamas latus rectum (tai direktrisei lygiagreti per židinį einanti styga, a - parabolės parametras).
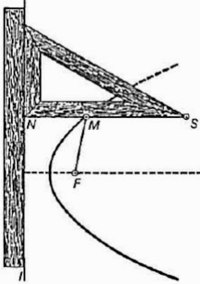
Parabolės, kurios šakos nukreiptos į viršų, lygtis būtų x2=4ay. Jei parabolės viršūnė yra taške (x0, y0), tada parabolės lygtis (su šakomis į dešinę): Paaiškinimas (1) lygtis išvedama žinant, kad stačiojo trikampio įstrižainės (c) ilgis randamas sprendžiant lygtį c2=a2+b2, kur a ir b yra kraštinių ilgiai. Nuleidžiame statmenį iš taško P gaudami trikampį Tad trikampio įstrižainei FP (kuri lygi OP, pagal parabolės apibrėžimą) Poliarinėse koordinatėse, židiniui esant taške (0,0), parabolės lygtis būtų: Parabolės braižymas naudojant įtemptą siūlą Tam reikia liniuotės ir stačiojo trikampio, kurio viename iš smailiųjų kampų (iliustracijoje, S) pritvirtintas siūlas, kurio ilgis lygus statinio SN ilgiui. Kitas siūlo galas tvirtinamas brėžiamos parabolės židinyje F. Liniuotė pridedame prie direktrisės. Kitą stačiojo trikampio statinį priglaudžiame prie liniuotės ir slenkam palei ją. Pieštuko galu įtempiame siūlą ir prispaudžiame prie statinio SN. Trikampiui slystant palei liniuotę pieštuko smaigalys brėžia parabolę.Parabolės brėžiama kreivė Parabolės viršūnės brėžiama kreivė parabolei riedant tokia pat kita parabole yra cizoidė. Ją
naudojo senovės graikų matematikas Dioklas, spręsdamas kubo padvigubinimo uždavinį. Beje,
Dioklas nustatė, kad parabolės formos veidrodžiai spindulius nukreipia į židinį tai
aprašydamas veikale Apie uždegančius veidrodžius. Kitos kūgių kreivės Apskritimas - aibė taškų P plokštumoje, esančių pastoviu atstumu r nuo taško O vadinamo centru. Elipsė - aibė taškų P plokštumoje, kurių atstumų nuo dviejų fiksuotų taškų suma yra pastovi. Tiedu taškai vadinami elipsės židiniais, o juos jungiančios atkarpos vidurys vadinamas elipsės centru. Taškai, kuriuose tiesė (vadinama pagrindine ašimi), einanti per židinius, kerta elipsę, vadinama verteksu. Tiesė, einanti per centrą ir statmena pagrindinei ašiai, vadinama mažąja ašimi. Hiperbolė - aibė taškų P plokštumoje, kuriems absoliuti skirtumo atstumų iki dviejų fiksuotų taškų yra pastovi. Tie taškai vadinami židiniais ir vidurinis atkarpos, jungiančius židinius, taškas vadinamas centru. Atstumas nuo centro iki židinio vadinamas židinio gyliu. Tiesė, einanti per židinius, vadinama židinių (transverse) ašimi. Etimologija Reikšmės graikų kalboje: Tai gali būti susiję su jų židinių atstumu nuo viršūnės - didesniu, trumpesniu ar lygiu atstumui iki direktrisės. Arba kertančiai plokštumai - už kūgio (nes kerta kitą), netoliese (nukertant gabalą) ar nubėgant lygiagrečiai šalia. |
|
FAP.
|
Parabolės savybės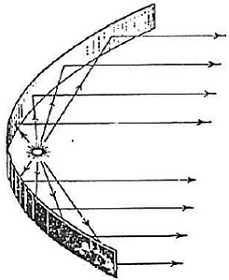 
1. Ploną, gerai šviesą atspindinčią juostelę (pvz., foliją) sulenkus parabolės forma, ir į ją nukreipus lygiagrečių šviesos spindulių pluoštą, atsispindėję spinduliai praeis pro židinį. Kita vertus, židinyje patalpinus šviesos šaltinį, nuo parabolės atsispindėję spinduliai sklis lygiagrečiai jos ašiai. Amerikietis Robertas Vudas, sukdamas indą su gyvsidabriu, sukūrė parabolinį veidrodį tai buvo puikus veidrodis. Jis panaudotas teleskopo gamybai. Jei paimtume labai didelį parabolinį veidrodį ir jį nukreiptumėm į saulę, tai židinyje susidarytų toks karštis, kad būtų galima lydyti plieną (lot. focus ir reiškia karščio šaltinį). Legenda pasakoja, kad Archimedas (287-212 m. pr.m.e.), gindamas Sirakūzus, romėnų laivyną sudegino naudodamas panašiais veidrodžiais (išdėstęs gerai nušlifuotus skydus - papildomai paskaitykite apie tokios galimybės įmanomumą). Tokia parabolinių veidrodžių savybė naudojama konstruojant saulės krosnis, teleskopus ir pan. Parabolinės radarų antenos į vieną tašką sutelkia radiolokatoriaus signalus, atsispindėjusius nuo skrendančių objektų. 2. Kampu mestas akmuo (ar patrankos sviedinys), svorio jėgos veikiamas, skrieja parabole. Tiesa, oro pasipriešinimas iškreipia trajektoriją. Jei sviedinys skrietų tuštuma, trajektorija būtų tiksli parabolė. Iššovus sviedinius tuo pačiu pradiniu greičiu, tačiau skirtingais kampais, gauname skirtingas paraboles, o sviediniai nulekia skirtingus nuotolius. Didžiausias atstumas vamzdį nustačius 45o kampu jis apytiksliai lygus v2 / g, kur g - laisvojo kritimo pagreitis. O štai šaunant vertikaliai aukštyn, sviedinys pakiltų į v2 / 2g aukštį, t.y. dukart mažesnį nei maksimalus nuotolis. Be to, esant tam pačiam pradiniam greičiui, kad ir kaip sukiotume patrankos vamzdį, ant
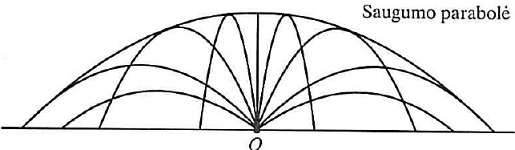
žemės paviršiaus ir virš jo bus vietų, kur sviedinys negali patekti. Šias vietas nuo pavojingų
zonų taip pat skiria parabolė, kuri vadinama saugumo parabole. Parabolės, kuriomis
skrieja sviediniai, liečia saugumo parabolę tad ji yra visų galimų parabolių gaubiamąja. Ją
nagrinėjant erdvėje gauname paviršių sukimosi paraboloidą.
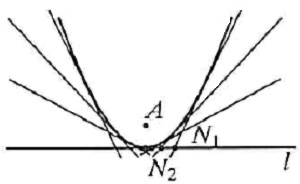
Vienuolis Bertoldas Švarcas 13-e amžiuje išrado paraką (žr. >>>>>). Pradžioje patrankos naudotos tik tiesioginiam šaudymui, be priedangos. Ištyrinėjus sviedinių trajektorijas, imta šaudyti iš už priedangų. Pirmasis tai tyrinėjęs matematikas buvo Nikolo Tartalja (1500-1577) iš Venecijos. Tačiau to meto mokslininkai nepripažino jo atradimų, kurie dabar vadinami kitais vardais. O ir Tartalja nežinojo dėsnių, kuriems paklūsta skriejantys sviediniai juos pirmąkart nustatė Galilėjus. 3. Parabolė kaip tiesių šeimos gaubiamoji Popieriaus lape pažymėkime tašką A ir greta jo nubrėškime tiesę l. Tada per kiekvieną tiesės l tašką N, nubrėžę tiesę, statmeną NA, gausime tiesių šeimą. Šių tiesių gaubiamoji yra parabolė.
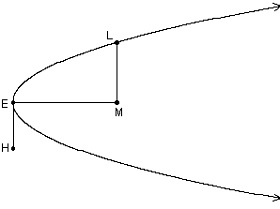
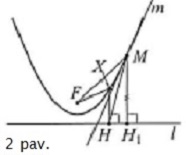
4. Parabolės židinio savybė Tegu F yra parabolės židinys, l direktrisė, X kažkuris parabolės taškas, o XH statmena l. Reikia įrodyti, kad parabolės lietinė taške X sudato vienodus kampus su tiesėmis XF ir XH (1 pav.). Įrodymas. Iš parabolės apibrėžimo turime XH=XF taigi X priklauso atkarpos FH simetrijos ašiai m. Įrodysime, kad ši simetrijos ašis ir yra parabolės liestinė, t.y. simetrijos ašis su parabole turi vieną bendrą tašką (X), o parabolė yra vienoje simetrijos ašies pusėje. Tiesė mdalija prokštumą į dvi dalis, kurių vieną sudaro taškai, esantys arčiau F negu H. Įrodysime, kad parabolė yra kaip tik šioje tiesės pusėje. Tegu M yra parabolės taškas (žr. 2 pav.), nesutampantis su X ir MH1 yra statmena
l. tada iš parabolės taškų savybės turime MH1=MF, kur MH1 yra M atstumas iki
l. Statmuo yra trumpesnis už pasvirąją, todėl MH1 < MH, t.y. kiekvienas
parabolės taškas (taškas M), išskyrus X, yra pusplokštumėje, kurią sudaro taškai, esantys arčiau
F negu H. Taškas X yra vienintelis vienodai nutolęs nuo F ir H. Įrodėme, kad
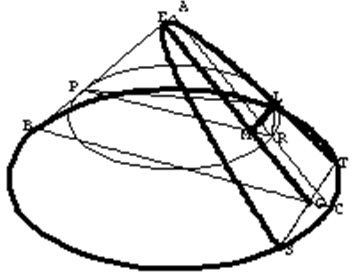
atkarpos HF simetrijos ašis m yra parabolės liestinė, o X - lietimosi taškas. Įrodymas apie kūgio pjūvį Teiginys: Kūgio pjūvis, kai kertančioji plokštuma yra lygiagreti šonui, yra parabolė.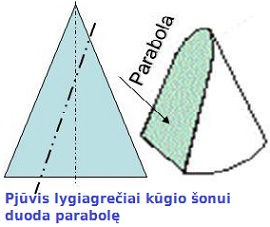 
Čia pateiksime Apolonijaus įrodymą.
Trikampiai PML ir LMR yra panašūs, o panašiems trikampiams galioja: Tada Apolonijus statmenai EM brėžia atkarpą EH, tokią, kad: Dabar panagrinėkime trikampius ABC, APR ir EPM kreivės ašies plokštumoje, Jie visi yra panašūs
pagal lygiagrečių tiesių savybes. Iš jų panašumo gauname: Apjungę (2), (3) ir (4) gauname: O kadangi EM yra lygiagreti AR (pagal mūsų pjūvio sąlygą), trikampyje APR turime: Įstatę (6) į (5), gausime: Kadangi akivaizdu, kad Iš (1) prisiminę, kad ML2 = PM * MR, turime O čia įvedus mums įprastus pažymėjimus y=ML, x=EM ir p=EX, gausime parabolės lygtį: Iš čia aiškėja, kodėl Apolonijus panaudojo žodį parabolė. Jis įrodė, kad ML kvadratas lygus
stačiakampiui, taikomam (paraboli) EH, kurio kita kraštinė yra EM. Tai remiasi plotų skaičiavimo
metodu, kurią graikai naudojo ilgių ir figūrų daugybai bei dalybai. Automobilio lempa - vienas parabolės savybių panaudojimo pavyzdžių... 1) Robertas Vudas (Robert Williams Wood, 1868-1955) amerikiečių
fizikas-eksperimentatorius ir išradėjas. Nuo 1935 m. Amerikos fizikų draugijos prezidentas. Pagrindine domėjimosi sritimi buvo optika:
jis atrado ir ištyrė optinį rezonansą, nustatė gyvsidabrio garų rezonansinį ultravioletinį spinduliavimą, atrado
rezonansinio spinduliavimo poliariškumą ir jo priklausomybę nuo magnetinio lauko, pradėjo
fotografuoti UV diapazone, kuriame pirmąkart padarė ir Mėnulio nuotraukas, sukonstravo Vudo lempą, skleidžiančią tik UV spindulius
ir naudojamą medicinoje, aptiko aukštą augalų atspindamąją galią infraraudonų spindulių diapazone (Vudo efektas) ir kt.
1909 m. sukūrė pirmąjį praktinį panauojimą turintį skysto gyvsidabrio parabolinį teleskopą ir
ištyrė jo privalumus ir trūkumus. Kartais jį laiko ašarinių dujų išradėju.
Kartu su A. Treinu parašė du mokslinės fantastikos romanus:
Žmogus, kuris sukrėtė Žemę (1915) ir jo tęsinį Antrasis Mėnulis (1916). Taip pat parašė ir iliustravo dvi knygas vaikams (1907-08). 2) Nikolo Tartalja (Niccolo Fontana Tartaglia, 1500-1557) italų
matematikas ir inžinierius, be matematikos nagrinėjęs ir praktinius topografijos bei balistikos klausimus.
Jau pirmajame savo traktate Nuova scienza nagrinėjo iššauto sviedinio trajektorijas. Jis nurodė, kad visa sviedinio trajektorija yra viena kreivė, o ne
dvi tiesios atkarpos, sujungtos viena kreive, kaip laikyta anksčiau. Taip pat užsiiėmė miestų fortifikacija. 3) Jakobas Šteineris (Jakob Steiner, 1796-1863) šveicarų
matematikas, daugiausia darbavęsis geometrijos srityje; 2-o ir aukštesnių eilių kreivių ir paviršių sintetinės geometrijos
pradininkas. Padarė svarbių tyrinėjimų ekstremumų (minimumų, maksimumų) srityje; nedidelis, bet
svarbus indėlis yra ir kombinatorikoje (dviejų puslapių straipsnyje išdėstęs tai, kas šiandien vadinama Šteinerio sistema). 4) Žeraras Desargas (Girard Desargues, 1591-1661) prancūzų
matematikas, geometras, inžinierius ir architektas, vienas projekcinės geometrijos pradininkų (1639 m. įvedė be galo
nutolusius objektus). Kaip architektas, Paryžiuje suprojektavo kelis privačius ir viešus pastatus, o taip pat vandens
pakėlimo sistemą. 1640 m. geometrinius metodus pritaikė praktiniams uždaviniams, susijusiems su saulės laikrodžiu ir akmenų pjaustymu.
Dažnai cituojamas yra jo juodraštinis variantas apie kūgio pjūvius plokštuma (1639). Jo garbei pavadintas krateris Mėnulyje. Taip pat skaitykite: |
Svaidyklių mėtomų svorių trajektorijomis domėjosi jau 
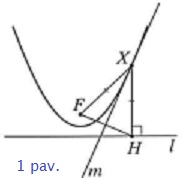
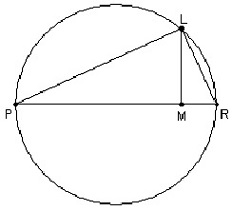Nuo kūgio skersmens PR iš taško M, esančio ant gautos kreivės ašies, iškelkime statinį ML. Turime
statųjį trikampį PLR, įbrėžtą į pusapskritimį. Pabandysime nustatyti sąryšius tarp ML ir EM (E yra kreivės viršūnė).
