|
Kampo trisekcija Uždavinio formulavimą ir negalimumo įrodymą skaitykite čia >>>> Kampo trisekcija skiriasi nuo kitų dviejų neišsprendžiamų uždavinių (skritulio
kvadratūros ir kubo padvigubinimo). Pirma, neturima istorijos, kaip klausimas buvo sprendžiamas. Antra,
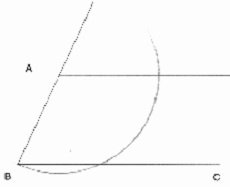
ji kitokio pobūdžio mat kai kuriuos kampus galima padalinti. Imkim kad ir statųjį kampą CAB. Nubrėškime du to paties spindulio apskritimus, kaip
parodyta brėžinyje. Tada trikampis DAE yra lygiakraštis, tad kampas DAE yra 60o, - o iš čia kampas DAC 30o. Papusas iš Aleksandrijos rašė: Tai rodo, kaip graikai patobulino kampo dalijimo sprendimus. Nuo mechaninio sprendimo jie perėjo prie kūgio pjūvių naudojimo. Beje, visai nesunku padalinti kampą pusiau. Kampui CAB atžymėkime lygias atkarpas
AB ir AC (brėžiant apskritimą), o tada nubrėžkime lygiagretainį CABD. Lieką nubrėžti įstrižainę kampo padalijimui pusiau. Noras kampą dalinti į bet kokį dalių kiekį susijęs su galimybe sudaryti bet kokius daugiakampius. Bet tik Gausas nustatė, kokius daugiakampius galima nubrėžti naudojant liniuotę ir skriestuvą. Sunku tiksliai pasakyti, kad iškilo kampo dalijimo problema, tačiau žinome, kad tai nagrinėjo Hipokratas iš Chijo. Jo metodas buvo gana tiesmukiškas (įterpimo metodas). Duotam kampui CAB brėžiam CD, statmeną AB, o tada sudarom stačiakampį CDAF. Pratęsiam FC iki E, kur E
parinktas taip, kad HE=2 * AC. Tada kampas EAB lygus 1/3 kampo CAB. To įrodymui paimkim G esantį HE viduryje taip, kad HG=GE=AC. Kadangi ECH yra status kampas, CG=HG=GE. Tada
kampas EAB=kampas CEA + kampas ECG. Bet kadangi AC=CG, kampas CAG=kampas CGA. O tada kampas Tačiau šis metodas naudoja žymėtą liniuotę. Vis tik iš jo lengvai surandamas mechaniškas būdas. Tereikia liniuotėje pažymėti 2 * AC ilgio atkarpą, o tada slinkti liniuotę su viena žyme ant CD, o kita ant FC, kol liniuotė eis per A. Tačiau tai nepanaikino graikų susirūpinimo, nes tai išėjo iš klasikinių reikalavimų srities. Platonas perspėjo: Veikdamas mechaniniu būdu, ne vienas beviltiškai prarado tai, kas geriausia geometrijoje... Yra žinoma, kad neįmanoma padalinti duotą kampą į tris lygias dalis naudojant tik nesužymėtą liniuotę ir skriestuvą. Tačiau palikus klasikinės graikų geometrijos ribas, yra dvi metodų, tai leidžiančių padaryti, klasės. Pirmąja yra neusis arba ribojančios konstrukcijos. Šio metodo tikslas duoto ilgio atkarpą įterpti tarp dviejų kreivių taip, kad toji atkarpa arba jos pratęsimas praeitų per duotą tašką. Kita metodų rūšis naudoja specialias kreives. Iš jų garsiausios Hipijaus kvadratriksė, Paskalio limakonas, Maclauri trisektrisė ir Archimedo spiralė. Iš jų kvadratriksę ir spiralę galima panaudoti kampo dalijimui į bet kokį lygių dalių skaičių. Archimedas pateikė vieną taisykles pažeidžiantį sprendimą [nors Hipokratas iš Chijo dar anksčiau pasiūlė sprendimą, tačiau jis remiasi kitu principu ]. Archimedo būdas 1. Paimkime kampą, kurį norime padalinti, ir iš taško A nubrėškime tiesę, lygiagrečią BC 2. Paimkite skriestuvą ir iš taško A nubrėžkite apskritimą spinduliu |AB| 3. Liniuotėje pažymėkite atstumą, lygų |AB|. Vieną liniuotės galą fiksuokite taške B. Pažymėkite D susikirtimo tašką su
mūsų nubrėžta linija (kuri lygiagreti BC). Tegu E būna BD susikirtimo tašku su nubrėžtu apskritimu. 4. Kampas BDA yra lygus trečdaliui kampo ABC. Pagrindimas. Kadangi BC ir AD yra lygiagrečios, kampai ADB ir DBC yra lygūs. Tada jiems lygus ir kampas EAD,
nes AE=DE. Tegu tie kampai lygūs a. Tada kampas AED = p - 2a.
Taigi, kampas AEB = 2a, ir kadangi |AB|=|AE|, tai ir ABE=2a. Kadangi kampams ABE+DBC=ABC, o kampas ABE=2a, tada kampas DBC=a Šis metodas aprašytas arabiškoje Lemų knygoje**) , kuri priskiriama Archimedui. Tačiau tikrai, tai nėra Archimedo traktato vertimas, nes keliose vietose cituojamas pats Archimedas. Sunku įsivaizduoti žmogų, kuris cituotų pats save. Vis tik istorikai mano, kad toji knyga aprašo Archimedo pasiekimus, nes pateikta kampo trisekcija savo dvasia labai atitinka Archimedo veikalą Apie spirales. Kitas metodas nenaudoja žymėtos liniuotės, o remiasi kreive, vadinama Hipijaus kvadratikse.
Jis leidžia kampą padalinti į kiek norima lygių dalių. Kvadratriksės sudarymas paprastas. Tegu A yra kampas, kintantis nuo 0 iki p/2,
o y = 2A/p. Pvz., kai A=p/2, tada y = 1, o kai A=0, tada y = 0.
Tada nubrėžkime horizontalią tiesę y=2A/p ir kampą A. Gausime susikirtimo tašką. Visų susikirtimo taškų,
kai A kinta nuo 0 iki p/2 visuma ir sudaro Hipijaus kvadratriksę. Dabar dalinsime kampą AOB. Hipijaus kvadratiksės formulė yra
x=y*cotang (p*y/2). Joje laisvu kintamuoju yra vertikali koordinatė y.
Dabar formulės patvirtinimas. Gretimame brėžinyje B=(x,y) yra Hipijaus kvadratriksės taškas. Tegu BO yra atkarpa iš koordinačių pradžios taško iki B, o BOC mūsų duotas kampas A. Jei tada nubrėšime apskritimą ir iš susikirtimo su kampo kraštine nuleisime vertikalę, gausime panašius trikampius ir
matysime, kas sin(A)/cos(A)=y/x arba tang (A)=x/y. Tačiau anksčiau ant kvadratriksės paėmėme tašką (x,y), tenkinantį
y=2A/p. Tad gauname tang(p*y/2)=y/x, kas ekvivalentiška x=y*cotang(p*y/2). Nikomedas gyveno beveik to pat metu kaip Archimedas (2 a. pr.m.e.), įvedęs kokleoidę siekdamas formalizuoti liniuotės sukimą išlaikant tašką ant linijos. Liniuotėje pažymėta tam tikra atkarpa ir viena atžyma išlaikoma ant linijos, o kita brėžia kokleoidę. Ją galima panaudoti kampo trisekcijai tai aprašė Papusas. Jis aprašė, kaip kampo trisekciją sprendė Apolonijus, (262-190 m. pr.m.e.), panaudodamas kūgio pjūvius. Jis pateikia du metodus, - abu naudojant hiperbolę [ hiperbolę galime apibrėžti kaip geometrinę vietą taškų kurių atstumų iki duotojo taško (židinio) ir duotosios tiesės (direktrisės) santykis yra pastovus ir lygus e > 1 (ekscentricitetas) ]. Piešinys kairėje parodo, kad fiksuotai linijai AB taškų P, kuriems 2 * kampas PAB=kampas PBA (t.y., PBA dukart
didesnis už PAB), visuma yra hiperbolė, kurios ekscentriškumas yra 2, židinys B, o direktrisė statmena AB vidurio taške.
To įrodymui svarbi jos savybė, kad 2*kampas PAB=kampas PBA. Tačiau 2*kampas PAB=kampas POB ir 2*kampas PBA=kampas POB (kampas iš centro yra dukart didesnis už kampą and to paties lanko). Tad 2*kampas POB=kampas POA. 
*) Kokleoidė - plokščia transcendentali kreivė, kurios lygtis poliarinėse koordinatėse r=a*sin(q), savo forma primenanti sraigę. Tai atvirkštinė kreivė Hipijaus kvadratiksei. **) Lemų knyga - knyga iš 15-os teoremų apie skritulius ir apskritimus, kurią Sabitas ibn Kura (836-901) priskyrė Archimedui, tačiau jo autorystė ginčytina. Joje yra įvestų naujų figūrų: arbelos (panašios į batsiuvio peilį), salinonas (druskos rūsys). 1661 m. išversta į lotynų kalbą. Papildoma literatūra:
Taip pat skaitykite: |