|
2019 metai matematikoje 2019-ais matematika pateikė atsakymų (bent jau dalinių) į keletą dešimtmečius matematikus kankinančių
iššūkių jau neskaitant virusinių problemų, vertusių rautis plaukus nuo galvų, ant kurių ir taip plaukų jau
nelikę (pvz., kam lygu 8÷2(2+2)?). Pirmiausia paminėsime, kad M. Griffinas, Ken Ono, Don Zagier'is ir L. Rolenas įrodė kažką, kas betarpiškai siejasi su Rymano hipoteze, laukiančia įrodymo dar nuo 1859-ųjų (trumpai apie tai >>>>>). Išsemti visi skaičiai iki 100 ieškant bet kurio skaičiaus išreiškimo trimis kitų skaičių kubais. Pasitelkus kompiuterius pagaliau buvo rastos 33 ir 42 išraiškos (žr. >>>>>). Nors pati hipotezė lieka neįrodyta. 2019 m. rugsėjį priartėta ir prie Collatzo teiginio įrodymo su Terrence Tao pasiektais rezultatais. Šis teiginys kabo ore dar nuo 1937 m., - ir mūsų svetainė vis dar nepateikė jo pristatymo :( O teiginio esmė yra ta, kad vadinamoji Sirakūzų seka galiausiai baigiasi 1. Hao Huangas iš Emory un-to 2019 vasarą paskelbė įrodęs beveik tris dešimtmečius (nuo 1994 m.) buvusią atvirą kompiuterių teorijos (informatikos) vadinamąją jautrumo problemą (jos esmė kiek reikia vieno bito pakeitimų, kad loginė funkcija pakeistų reikšmę). Kirigami (popieriaus karpymas) mažiau žinomas nei origami (popieriaus lankstymas), tačiau abu randa pritaikymų pramonėje. Harvardo matematikai išvystė kirigami pritaikomą matematiką, atskleisdami naujus aspektus gamybai ir medžiagų moksle. Jie sukūrė matematinę teoriją, parodančią, kaip bet kurį medžiagos lakštą galima transformuoti į bet kurią norimą formą. Nuo 1960 m. buvo vis greitinamas daugybos algoritmas kol pagaliau 2019 m. kovą pasiektas N
log(N) lygis ir laikoma, kad greitesnio jau būti negali. Daugiau skaitykite>>>>>
Įdomus sprendimas pateiktas ir parodant kaip galima aproksimuoti pi (ar bet kurį kitą iracionalų skaičių), žr. >>>>> Po kelių dešimtmečių tylos pagaliau 2019-ais pastebėtas progresas Saulėgražos teiginio, suformuluoto P. Erdošo 1960-ais, įrodyme. Prieš tai tebuvo viena publikacija 1997-ais, ir nauja pasirodė 2019-ais, paskui kurią jau pasekė ir kitos (Anup Rao). Ramsey teorijoje matematikai ieško nuspėjamų dėsningumų dideliuose chaotiškų duomenų kiekiuose. Ir pagaliau gautas atsakymas į vieną 1969-ais iškeltą klausimą: ar egzistuoja visad laimintis loterijos bilietas? Per visus 3000 metus niekas nepastebėjo paprasto kvadratinės lygties sprendimo būdo, kurį, galiausiai, 2019 m. gruodį paskelbė Po-Šen Lohas. Apie jį skaitykite >>>>> Pirmąkart prestižiškiausią tarp matematikų Abelio premiją gavo moteris, amerikietė Karen Uhlenbeck, daugiau apie tai >>>>> 2018 metai matematikoje Kuo toliau, tuo labiau norisi skaičiuoti viščiukus. Ypač metų pabaigoje... Prieš tai jau peržvelgiau už ką buvo skirtos 2018 m. Nobelio fizikos premijos (skaitykite Manipuliacijos šviesa), o dabar žvilgsnį nukreipiau į matematiką (kartu šiek tiek ir kompiuteriją paliesdamas) žinia, juk matematiką Nobelis pamynė neskirdamas premijos dėl meilės trikampio reikalų (apie tai žr. >>>>>). Šiemet vyravo jaunimas. Vienas iš keturių Fieldso medalio, skiriamo matematikams iki 40 m. amžiaus, laureatų buvo 30-metis Peter Scholze1), tapęs jauniausiu jį gavusiu (priešingai nuo A. Aškino, kuris buvo seniausias). Tačiau 2018-ais net ir 30-metis galėjo atrodyti labai senas... Du studentai, kurių vienam tebuvo 18-a, dviem atskirais atradimais perstumdė ribas, kvantinius kompiuterius skiriančias nuo įprastinių skaičiavimų. O kitas įrodė dešimtmečius ramybės neduodantį teiginį apie elipsines kreives. O ir visų amžių grupių matematikos mėgėjų indėlis buvo svarus ilgai neišsprendžiamų problemų srityje. Tačiau ko gero reikšmingiausiu jaunimo iškilimo ženklu buvo tai, kad minėtas P. Scholze, nepraėjus nė mėnesiui po Fieldso medalio gavimo, kartu su bendradarbiu padarė viešą pareiškimą, nurodydamas spragą garsiojo ABC teiginio įrodyme, kuris jau 6-i metai niekaip nepatikrinamas. Viltys dėl kvantinių skaičiavimų palaidotos? 2018 m. bus pažymimi tuo, kad pagaliau pademonstruota, kad kvantiniai kompiuteriai nėra pranašesni už tradicinius. Iki tol tai dar buvo neaišku - tai paaiškėjo, kai liepą 18-metis Ewin Tangas išeliminavo, kaip atrodytų, aiškiausią ir geriausią uždavinį, atseit parodantį kvantinių kompiuterių pranašumą... (žr. >>>>>) Tai rekomendacijos uždavinys, kurio praktinio panaudojimo išraiška, pvz., būtų, kaip Amazon nustato, ką dar jums būtų verta pasiūlyti įsigijimui. Tradiciškai laikyta, kad kvantiniai kompiuteriai jį turėtų spręsti žymiai (eksponentiškai) sparčiau. Dar 2014 m., būdamas 14 m. amžiaus ir praleidęs 6-ias klases, Tangas tapo Austino un-to studentu ir 2017 m. ėmė lankyti S. Aaronsono kvantinės informatikos kursą. Pamatęs gabų studentą, Aaronsonas pasisiūlė jam vadovauti. Tangas pasirinko rekomendacijos uždavinį. 2016 m. I. Kerenidis and A. Prakashas buvo paskelbę (žr. >>>>>) jo sprendimo kvantinį algoritmą, ... tik jie neparodė, kad negali egzistuoti spartesnis klasikinis algoritmas. Ir pradžioje E. Tangas bandė įrodyti, kad toks greitesnis klasikinis algoritmas yra neįmanomas. Kai tai jam nesisekė, jis pradėjo manyti, kad vis tik jis įmanomas. Ir jam pavyko sukurti algoritmą, įvykdomą per polilogaritminį laiką (t.y., kaip ir kvantinis algoritmas). Jį pristatė birželio viduryje Kalifornijos un-to kvantinių skaičiavimų workshope. Šis rezultatas netgi leido kai kuriems mokslininkams teorizuoti, kad kvantiniai kompiuteriai niekada nebus pranašesni už tradicinius. Taip pat skaitykite Kliūtys kvantinių kompiuterių kelyje Susirungė matematikos titanai Matematinis įrodymas yra arba teisingas, arba jį dar reikia patobulinti. Tai teoriškai, o praktikoje įrodymai gali
atrodyti labai logiški, tačiau matematikai irgi žmonės. Tai ypač išryškėjo prieštaravimuose, susijusiuose su
ABC teiginiu, vienu pagrindinių skaičių teorijoje. Jo įrodymą dar 2012 m. paskelbė
japonas Š. Mochizuki, tačiau nuo tada tik keli matematikai įstengė prasekti milžiniško dydžio sunkiai suprantamą įrodymą. Ir gegužę
P. Scholze ir J. Stixas iš Gėtės un-to Frankfurte pareiškė, kad jie atrado rimtą, nepašalinamą spragą jo įrodyme.
Tačiau Mochizuki tebetvirtina, kad įrodymas teisingas, tik jie nesuprato jo teorijos. Mašininis apsimokymas atsitrenkė į dramblį Dirbtinis intelektas (DI), sustiprintas mašininiu apsimokymu, 2018-ais tebebuvo
ant bangos. Tačiau kartu tyrinėtojai perstumdė ribas, ties kuriomis užstringa net ir išmaniausios DI sistemos. Viena jų grupė aptiko (žr.
>>>>>), kad patikima vaizdų atpažinimo programa keistai suklumpa nepastebėdama
dramblio kambaryje (nors tai nesudaro jokio vargo vaikui). Programai jie pasiūlė įprastinio kambario vaizdą ir ji
teisingai atpažino daiktus: kėdę, žmogų, knygas lentynoje... Tada tyrinėtojai kambario vaizdą papildė neįprastu objektu
nedidelio dramblio atvaizdu. Ir programos atpažinimas staiga nusimušė: ji kėdę pradėjo vadinti sofa, o dramblį
kėde, ir nustojo pastebėti kitus daiktus, kuriuos anksčiau atpažino kambaryje. Jie keitė dramblio vietą vaizde, ir
programa vis tiek tebekvailiojo. Tyrinėtojai atliko daugiau bandymų, ir nustatė, kad programa pasimeta ir tada, kai
padubliuojamas jau esantis vaizde daiktas, pvz., šuo, televizorius... Krito ir kvantinės verifikacijos problema 2017 m. spalį 28 m. amžiaus indų kilmės Urmila Mahadev pateikė svarbaus kvantinės informacijos teorijos klausimo (kvantinio verifikavimo) sprendimą (žr. >>>>>). Ji studentaudama Berklio Kalifornijos un-te 8 m. praleido tirdama, kaip kvantiniai kompiuteriai panaudoja kvantiškumą uždavinių sprendimui. Ji sugebėjo rasti kvantinių skaičiavimų pritaikymą kriptografijoje visiškai nauju būdu. Jų slaptos būsenos (kurios žinomos verifikatoriui, tačiau nežinomos kvantiniam kompiuteriui) procedūra remiasi spąstų funkcija (kurią lengva realizuoti, tačiau sunku gauti atvirkštinę funkciją; pvz., gauti skaičių, kuris kurio kvadratas yra 9 - tai gali būti ir 3, ir -3). Dominantis klausimas toks: jei nurodote kvantiniam kompiuteriui spręsti kokį nors uždavinį, kaip galite patikrinti, ar jis tikrai vykdo jūsų nurodymus, ar tik kažką savaip kvantiškai veikia? Juk jei kvantiniai kompiuteriai gali išpręsti tokius uždavinius, kurie neįveikiami klasikiniams kompiuteriams, kaip sužinoti, ar jie veikia teisingai? Juk vidinės kompiuterio būsenos yra daugybės skirtingų nekvantinių būsenų (panašių į Šriodingerio katiną, kuris tuo pačiu metu ir gyvas, ir negyvas) pasekmė. Antrais studijų metais (2012) Mahadev įsitraukė į šią problemą, nes ji jos gerai nesuprato ir po 7 m. užsispyrimo pasiekė rezultatų ir juos 2018 m. pristatė konferencijoje Paryžiuje, gaudama geriausio darbo įvertinimą. Jos verifikacijos protokolas rėmėsi prielaida, kad kvantinis kompiuteris negali pralaužti LWE, kuris, kaip manoma, įsigalios post-kvantinėje kriptografijoje. Begalinės kreivės yra dviejų tipų Elipsinės kreivės yra svarbūs matematiniai objektai, pasižymėję tokiuose įrodymuose, kaip Ferma teorema. 2017 m. atspausdintas nelabai pastebėtas Harvardo un-to studento Alexander Smitho straipsnis (žr. >>>>>), įrodantis 40 m. senumo teiginį, kad lygiai pusė elipsinių kreivių turi vadinamąjį rangą lygų 0, o kita pusė - 1 (nepaisant to, kad yra begalinis elipsinių kreivių su rangu 2 ir didesniu). {Rangas yra kreivės racionalių sprendinių aibės matas. Nors kreivių su rangu >=2 yra begalinis kiekis, tačiau iš tikro jų santykis su turinčiomis rangus 0 ir 1 yra toks mažas, kad tokias galima ignoruoti}. Mėgėjas rado mažiausią padengimą Matematikos mėgėjams 2018 m. irgi buvo vaisingi. Australų fantastas Greg Eganas padarė proveržį su perstatomis susijusiame uždavinį, neišsprendžiamame jau 25 m. 2011 m. rugsėjo 16 d. fanatikas 4chan forume uždavė klausimą apie TV serialą Haruhi Suzumiya melancholija. Pirmojo sezono serijos, kuriose vyksta kelionės laike, buvo parodytos nechronologine tvarka, o vėliau pakartotos ir įrašytos į DVD kita tvarka. Fanatikai ginčijosi, kokia tvarka geriausia žiūrėti serijas - ir buvo paklausta: Jei norima peržiūrėti serijas kiekviena įmanoma tvarka, koks yra trumpiausias epizodų, kuriuos jiems būtina žiūrėti, skaičius. Jau per pirmą valandą anoniminis komentatorius pateikė apatinę įverčio ribą (93,884,313,611). Tačiau klausimas išsprūdo iš profesionalių matematikų akiračio. Vis tik spalį G. Eganui pateikus naują viršutinės ribos įrodymą, jų susidomėjimas atsinaujino ir jie juos patikrino. Pasirodo, abu tiedu įrodymai priartino 25 m. senumo uždavinio sprendimą. O biologas Aubrey de Grey, prieš senėjimą kovojančios organizacijos vienas įkūrėjų (jis tvirtina, kad žmonės gali gyventi iki 1000 m.), pastūmėjo į priekį uždavinį apie chromatinį plokštumos laipsnį, užsistovėjusį jau 60 m. 1950 m. studentas Edward Nelsonas uždavė gana paprastai skambantį klausimą, kuris, vienok, matematikams kelis kitus dešimtmečius kėlė galvos skausmą. Paimkim grafą (taškus, sujungtus linijomis) plokštumoje, kurio visos briaunos vienodo ilgio. Tada nuspalvinkim jo viršūnes taip, kad jokios gretimos nebūtų tos pačios spalvos. Kiek mažiausiai spalvų pakanka tokio grafo nuspalvinimui? Klausimas prikaustė daugelio matematikų, įskaitant garsųjį P. Erdošą, dėmesį. Jie greitai susiaurino atsakymų ribas, nustatę, kad begalinis grafas gali būti nuspalvingas ne mažiau nei 4 ir ne daugiau nei 7 spalvos. O toliau reikalai sustojo ir tos ribos nekito, kol balandį Aubrey de Grey paskelbė straipsnį (žr. >>>>>), kuriame nurodė, kad mažiausias chromatinis skaičius yra 5. Į matematiką jis įsitraukė ... per Reversi (Othelo) žaidimą. Tarp žaidėjų buvo matematikų, kurie jį supažindino su grafų teorija. Uždavinio sprendimui jis panaudojo kompiuterį ir nustatė, kad grafo su 1581 viršūnėmis nuspalvinimu nepakanka 4 spalvų. Vėliau (jau kitų entuziastų) buvo surandami mažesni 5-ių spalvų reikalaujantys grafai. 2018 m. pabaigoje jau buvo turimas toks grafas su 553 viršūnėmis. Ir galiausiai 2006 m. į pensiją išėjęs programuotojas Philip Gibbsas pagerino mažiausią šimtmetį ieškomą visatos padengimą mažiausio ploto objektą, kuris gali uždengti bet kurią kitą dvimatę figūrą. Ph. Gibbsaas buvo gavęs teorinės fizikos daktaro laipsnį, tačiau neužsiėmė akademine veikla, o programavo laivus, oro skrydžių valdymo ir finansines sistemas. Tačiau išliko susidomėjimas mokslu, tik laiką galėjo skirti kažkokiai nišinei problemai. Ir dar jis jautė, kad jam gali padėti programavimo įgūdžiai. Šį uždavinį 1914 m. pasiūlė prancūzas Henri Lebesgue2) laiške savo draugui Julius Palui, tačiau progresas jį sprendžiant buvo labai lėtas iki pat Gibbso proveržio. Įsivaizduokite tuziną popieriaus karpinių ant grindų įvairaus dydžio ir formų. Tada jus paprašo surasti figūrą, kuri
būtų pakankama, kad galėtų uždengti bet kurią iškarpą. Ir toji privalo būti mažiausio ploto! Tokia Lebesgue uždavinio
esmė, pridedant sąlygą, kad bet kurie du uždengiamos figūros taškai yra mažesniu už 1 atstumu. Tokių figūrų yra
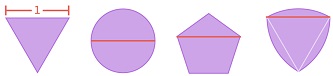
daugybė ir sunku rasti vieną universalų uždangalą visoms joms. Kaip kelis pavyzdžius, pateiksime lygiakraštį
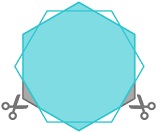
trikampį, skritulį, taisyklingą penkiakampį ir Reuleaux trikampį. Gavęs laišką, Palas greitai surado šešiakampį, tinkantį būti universaliu uždangalu. Tačiau vėliau jis jį padidino, pastebėjęs, kad gali, pasukęs 30o, nukirsti du gretimus apatinius kampus ir turėti mažesnio ploto figūrą, galinčią uždengti minėtas figūras. Ties tuo jis ir sustojo. Per kitus 80 m. dar du matematikai sugebėjo kai ką iš jos nukirpti: Roland Sprague (1936) ir H. C. Hansenas (1992). Susidomėjimą uždaviniu atgaivino Dž. Baezas, apie jį 2013 m. parašęs savo populiariame bloge. Tai perskaitęs, Ph. Gibbsas 2014 m. atliko kompiuterines simuliacijas su 200 atsitiktinai sugeneruotų formų. Jos parodė, kad iš ankstesnio mažiausio uždengimo galima nukirpti kažkiek nuo viršutinio kampo. Įrodymą jis nusiuntė Dž. Baezui, kuris paprašė savo studentę Karine Bagdasaryan padėti Gibbsui parengti labiau formalizuotą įrodymą. 2015 m. vasarį šis trejetas paskelbė straipsnį (žr. >>>>>), kuriame padengimo pagerinimas nuo ankstesnio buvo 0,0000224. Gibbsas nenurimo ir spalį pasiūlė dar vieną pagerinimą (žr. >>>>>). Jis tebemano, kad padengimą dar galima pagerinti. O Dž. Baezas tikisi, kad Gibbso entuziazmas pritrauks ir kitų matematikų dėmesį. 1) Piteris Šolcas (Peter Scholze, g. 1987 m.) vokiečių matematikas, žinomas indėliu į skaičių teoriją ir aritmetinę geometriją (pvz., p-adinę geometriją ir jos taikymus), Bonos un-to prof. (nuo 2012 m. 24 m. amžiaus tapęs jauniausiu profesoriumi Vokietijoje), Fieldso medalio laureatas (2018). 2018 m. paskirtas M. Planko vardo matematikos instituto direktoriumi. Išgarsėjo 2011 m. straipsniu apie perfektoidines erdves. 2) Anri Lebegas (Henri Leon Lebesgue, 1875-1941) prancūzų matematikas, vienas realaus kintamojo
funkcijų teorijos kūrėjų. Žinomas kaip Lebego mato ir juo besiremiančio Lebego integralo, apibendrinančio integralo
sąvoką platesniam funkcijų ratui, teorijų autorius (1901). Jie įgavo paltų pritaikymą įvairiose matematikos srityse. Taip
pat įvedė sumuojamos funkcijos ir funkcijos beveik visur sąvokas. Prisidėjo ir prie kompleksinių skaičių teorijos ir
topologijos vystymo. Taip pat skaitykite: |
