Grandi paradoksas Kam lygu 1-1+1-1+1-1+... ir taip iki begalybės? Tokį uždavinį pirmąkart nagrinėjo italų vienuolis ir matematikas Gvido Grandi*). 18 a. jis sukėlė ilgą ir gyvą diskusiją.
Buvo siūlomi trys atsakymai: 0, 1 ir 1/2. Tačiau kuris iš jų teisingas?! Daugelis laikė, kad 1/2, ir net pateikdavo
įrodymus. Pvz., Leibnicas samprotavo taip: sudedant iš eilės gauname
1, 0, 1, 0 ir t.t., t.y. 0 ir 1 yra lygiaverčiai ir todėl jų vidurkis yra labiausiai tikėtinas rezultatas.
Oileris pasiūlė kitą paaiškinimą: geometrinės progresijos 1, -1, 1, -1,
, t.y., kai daugiklis lygus -1, suma lygi Pats Grandi, kurio vardu dabar vadinama ši eilutė, gavo du atsakymus: 0 ir 1. Tam jis dėmenis suskirstė poromis ir skirtingai sudėliojo skliaustelius: vienu atveju pradedant 1, o kitu pradedant -1. Ir tai jo nesutrikdė: teologas paėmė viršų prieš matematiką lygybė tarp 0 ir 1, jo nuomone, įrodo, kad pasaulis (1) buvo sukurtas iš nieko (0). Vėliau Grandi pripažino 1/2 ir tai pagrindė tokia alegorija. Tėvas dviem sūnums paliko brangakmenį. Pagal testamentą jo nebuvo galima padalinti ar parduoti. Metus jis
būna pas vieną brolį, o kitus metus pas kitą. Tad brangakmenį abu turės pusę viso laiko.
Deja, visi minėti asmenys klydo, nes pernelyg laisvai elgėsi su begalinėmis sumomis, joms priskirdami baigtinių sumų savybes. Tačiau iš esmės jokių apribojimų operacijoms su eilutėmis tuo metu dar ir nebuvo, o ir eilučių konvergavimo supratimas dar buvo nenusistovėjęs, kas dar labiau glumino matematikus. Jam atsiradus 19-me amžiuje ginčas buvo užbaigtas. Išaiškėjo, kad daugelis sumų neturi rezultato (matematiškai sakoma, kad jos diverguoja). Tokia yra ir Grandi eilutė kiek besumuotume jos narius, galutinio rezultato niekada negausime. Paprastai tokių eilučių sumavimas nedomina, tačiau kai kuriais atvejais vien analizės tikslais gali būti pritaikomi italo E. Cesaro (1859-1906) įvesti sumavimo metodai, skirti dalinių diverguojančių eilučių sumų suradimui (ne visoms diverguojančioms eilutėms galima rasti dalines sumas). Prabėgo tie 300 m. Ir jau mūsų laikais italų tyrinėtojai atliko eksperimentą: 88 mokiniams, kurių amžius 16-18 m., ir nesusipažinusiems su begalinių eilučių savybėmis, pasiūlė išspręsti šį uždavinį. Iš ką jūs manote? Nuomonės pasiskirstė taip: 0 29% (ir 18 iš 26 pateikė paties Grandi argumentus); 1 4%; 0 arba 1 20%; 1/2 5%; begalybė 2%; neįmanoma paskaičiuoti 6%; neatsakė 34%. 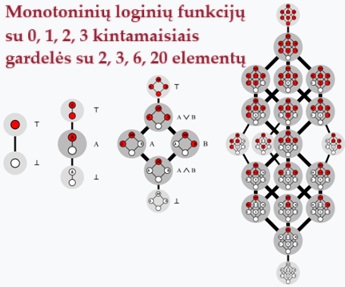
Devintukas tik po 32 m. Dedekindo skaičius - sveikas skaičius, žymimas M(n), nurodantis monotoninių loginių funkcijų kiekį esant n kintamųjų. Monotoninė funkcija funkcija, kuri savo apibrėžimo srityje vien tik didėja arba vien tik mažėja (pvz., ex). Ekvivalentiškas apibrėžimas: antigrandinių kiekis aibėje iš n elementų. M(n) seka labai sparčiai didėja ir nors žinomi asimptotiniai įverčiai bei tiksli išraiška sumos pavidalu, tačiau betarpiškai išreikštos paskaičiavimo formulės nėra. Jei n yra lyginis, tai ir M(n) yra lyginis. Tik 2023 m. paskaičiuota M(9) reikšmė (iš 42 skaitmenų): 2867 386 577 668 298 411 128 469 151 667 598 498 812 366. M(n) skaičių 1897 m. apibrėžė R. Dedekindas, paskaičiuodamas reikšmę M(4)=168. M(8) 1991-ais paskaičiavo superkompiuteris Cray-2. O tada M(9) po 32 m. pertraukos savarankiškai paskaičiavo dvi nepriklausomos matematikų grupės ir jų rezultatas sutapo. Kristianas Jakelis iš Vokietijos pritaikė formaliųjų sąvokų analizės techniką ir panaudojo grafinį greitintuvą (5311 valandos Nvidia A100 darbo). Kita grupė buvo iš Belgijos ir ji panaudojo 47 tūkst. specialios mikroschemos Stratix darbo valandų (apie 3 mėn.) valdant superkompiuteriui Noctua 2 Paderborno un-te. K Jakelis preprintą paskelbė 3 d. anksčiau už belgus... *) Guido Grandis (Luigi Guido Grandi, 1671-1742) italų vienuolis, teologas, matematikas ir
inžinierius. 1707 m. jau įgijo tokią matematiko reputaciją, kad buvo paskirtas Toskanos valdovo Kozimo III Medičio rūmų
matematiku, akrtu dirbdamas ir inžinieriumi, atsakingu už vandens tiekimą kunigaikštystei. Taip pat skaitykite: |