|
|
|
Skaitiniai |
Klaidžiojantis kvadratas Vienišas pėstininkas veržiasi į valdoves; jo karalius toli nepadės. Ar jis suspės, nusprendžia kvadrato taisyklė, t.y. ar varžovo karalius patenka į tą kvadratą. O jei pėstininkų ne vienas, o dvi? Štai tokiam atvejui ir išvesta klaidžiojančio kvadrato taisyklė, o kartu su ja ne mažiau sėkmingai gali būti taikoma ir septynių taisyklė... Pėstininkai būna įvairūs: sudvejinti, sujungti, atskirti viena ar keliomis vertikalėmis... Pradėkime sujungtais
pėstininkais, kurie šioje partijoje yra pas abu varžovus: Šioje padėtyje karalių galimybės ribotos: baltieji tegali vaikščioti po h1-g2 laukelius, kaip ir juodieji po a7-b6 (tiesa, juodieji dar gali eiti 1. ... c7, ta2iau tada tiesiog baltųjų pėstininkų konfigūracija po 2. a7 Kb7 3.b6 tik pasislenka aukštyn). Lygiosios! ir išvada: du sujungti pėstininkai gali užlaikyti priešininko karalių, tačiau be savo karaliaus paramos praeiti negali. O štai sudvejinti pėstininkai tradiciškai laikomi silpnais, tačiau, kaip ir visur, yra išimčių: Po baltųjų išlaukiamųjų ėjimų 1. Kb5 a5 2. Ka4 juodieji jau gali ir pasiduoti jų karalius privalo palikti pėstininko h6 kvadratą, o jų pėstininkas f7 yra kenksmingas be jo jie netgi laimėtų! O ar tokių padėčių būna etiuduose? Be abejo! štai A. Votavos etiudas (1937): Baltieji pradeda ir laimi: 1. c5 Kb4 2. c6 dc 3. e5 Kc5 4. e4 ir dėl savo lauką c6 blokuojančio pėstininko
karalius privalo atsitraukti (cugcvangas!) ir po 3 ėjimų lentoje pasirodo baltųjų valdovė: O ar buvo panašių padėčių praktikoje? Žinoma. Štai padėtis, iš kurios galima spręsti, kad varžovai žaidė labai
sentimentaliai ir daug dėmesio skyrė smulkmenoms ir čia nėra kuo stebėtis, nes žaidė moterys Borisenko-Zvorykina (Ryga, 1962): O toliau įvykiai vystėsi taip: 38. ... V:f4+ 39. K:f4 a4! 40. Ke4 b4 41. K:d4 ba 42 Kc3 Kg5 43. d4 K:g4 Baltųjų karalius prikaustytas prie laukelio c3, tad judėti gali tik pėstininkas d, tačiau juodųjų karalius netrunka jį suėsti. Baltieji pasidavė! O dabar pažiūrėsime padėtis, kai pėstininkus skiria viena vertikalė, pvz., Po 1. Kc4 a4 2. Kc3 Kh5 3. f5 Kh6 lentoje nusistovi dinaminė pusiausvyra: pėstininkai negali judėti, o
karaliai manevruoja tais pačiais laukeliais (c4,c3 ir h5,h6) lygiosios! O jei vis tik kuri nors pusė (tarkim baltieji) nuspręstų pažeisti pusiausvyrą ir pasuktų į kairę, štai kas nutiktų:
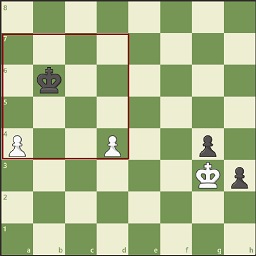
4. Kb2?! c4! 5. Ka3 c3 6 Ka2 pozicija valdovės sparne veidrodiškai pasislinko žemyn: Ir čia jau baltiesiems ne juokai galvoje po 6. ... Kh5 7. Kb1?? a3 jie patenka į cugcvangą! (tiesa, baltuosius dar gelbsti 7. Ka3) O dabar pažvelkime į senų laikų P. Kareros poziciją (1617), kurią reiktų žinoti kiekvienam šachmatininkui-praktikui. Joje po bet kurio juodųjų karaliaus ėjimo vienas iš baltųjų pėstininkų prasiveržia į valdoves, o tuo tarpu baltųjų karalius susitvarko su juodųjų pėstininkų falanga tačiau rezultatas priklauso nuo pirmojo baltųjų ėjimo! 1. Kg1! vienintelis ėjimas, nes po 1. Kg2 g3! Baltiesiems cugcvangas. 1. ... h3 2. Kh2! f3 3. Kg3 h2 4. K:h2 f2 5. Kg2 g3 6. Kf1 Iš čia matome, kad nors atskirti pėstininkai savarankiškai į valdoves praeiti negali, jie turi gynybinių priemonių ir gali užlaikyti varžovo karalių prie savęs kaip ir esant sujungtiems pėstininkams. O dabar tegu pėstininkus skiria dvi arba daugiau vertikalių. Jiems sugalvota klaidžiojančio kvadrato taisyklė (A. Studeneckis, 1939 m.). Tai kvadratas su kraštine, lygia atstumui tarp pėstininkų ir jis juda kartu su pėstininkais. Jei tasai kvadratas pasiekė lentos kraštą ar išėjo už jos ribų, tai kažkuris pėstininkas praeina į valdoves. Jei ne tada karalius sulaiko pėstininkus. Šioje pozicijoje klaidžiojantis kvadratas pasiekė kraštą: Taigi, nepriklausomai, kurios pusės ėjimas, vienas iš baltųjų pėstininkų praeis į valdoves. Baltųjų ėjimo atveju: 1. d6! Kc6 2. a6! K:d6 3. a7. Juodųjų ėjimo atveju 1. ... Kc8 2. a6 Kc7 3. a7 Kb7 4. d6! K:a7 5. d7 Jei poziciją valdovės sparne stumtelėsime viena eilute žemiau, tai rezultatas bus kitoks! Pėstininkai žūva neparodę jokių gynybinių požymių dviejų langelių atstumas tarp pėstininkų yra mažiausiai naudingas. Jei baltieji pradeda 1. d5, tai seka 1. ... Kc5 laimint d pėstininką ir juodieji spėja įšokti į a pėstininko kvadratą. O jei ėjimas juodųjų, tai jie žaidžia 1. ... Ka5 2. d5 Kb6! 3. Kh2 Kc5 (tik ne 3. ... K:a4, nes 4. d6 ir pėstininkas nepavejamas). O tokia pozicija susidarė Štolco-Nimcovičiaus partijoje (1928): Sekė 1. ... f4! 2. gf+ Kd6!! (grubi klaida būtų 2. ... K:f4, po kurio baltųjų pėstininkas praeina su šachu ir baltieji laimi). Dabar juodųjų pėstininkai nesulaikomi, o bet kuris baltųjų pėstininkas sustabdomas. Tad juodieji sparčiai nuskuba su pėstininkais ir laimi: 3. a5 (arba 3. f5 g3 4. Ke1 d3 5. f6 g2 6. Kf2 d2 7. f7 g1V+ 8. K:g1 d1V+) 3. ... g3 4. a6 Kc7! 5. Ke2 d3+ 6. K:d3 g2 su lengvu laimėjimu. Klaidžiojančio kvadrato taisyklė turi alternatyvą septynių taisyklę, įvestą prancūzo Šerono: pėstininkai praeina į valdoves, jei jas skiriančių laukų kiekis ir eilutės numerio suma ne mažesnė nei 7. Pažiūrim į Štolco-Nimcovičiaus poziciją: pėstininkus (po antro ėjimo) skiria du laukai, o jie pasiekė 5-ąją horizontalę, ką sudėjus kaip tik gauname 7. O jų kvadratas iš tiesų pasiekęs lentos kraštą. |